



Next: M-6 Uniform Circular Motion
Up: PHYS 201/202 and 207/208
Previous: M-4 Acceleration in Free Fall
OBJECTIVE: To find the initial velocity and predict the range of a
projectile.
APPARATUS:
Ballistic pendulum with spring gun and plumb bob,
projectile, single pan balance, elevation stand.
PART I. BALLISTIC PENDULUM
Figure 2:
A side view of the catcher
Figure 1:
The spring gun.
![\begin{figure}
\centering
\includegraphics [height=2.70in]{figs/l103/m05-3.eps}...
...
\centering
\includegraphics [height=1.70in]{figs/l103/m05-r4.eps}
\end{figure}](img120.gif) |
INTRODUCTION:
*.3in
A properly aligned spring gun shoots a ball of mass
m into a pendulum of mass M. See Figs. 1 and 2. The
pendulum traps the ball;
thereafter the two move together in pure translation. Since ball and
pendulum have no
relative motion, the collision is inelastic and thus does not conserve
mechanical energy (where does it go). Of course
linear momentum is still conserved, and hence momentum of ball before
impact, mu, equals the momentum of ball plus pendulum after impact,
(m+M)V:
where u = ball's velocity before impact
and V = initial velocity of combined
pendulum plus ball.
*.3in
To find V, note that although the impact
doesn't conserve mechanical energy, the motion
after impact is almost frictionless and thus conserves
mechanical energy.
Hence the kinetic energy of the ball plus pendulum at A in Fig. 2, just
after impact, equals the potential energy of the two at the top of
the swing (at B). Thus
| 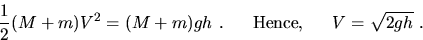 |
(2) |
Pre-lab Quiz
You should be able to complete this brief quiz before proceding.
Read the Introduction section carefully, especially if
you are unfamiliar with the concepts of conservation of energy and momentum.
ALIGNMENT:
*.3in
If properly aligned, our bifilar type
of suspension for the pendulum
(see Figs. 1 and 2) prevents rotation of the bob of mass M. Hence the
motion is pure translation.
To ensure proper alignment, adjust the three knurled screws in base so that
- 1.
- A plumb bob hangs parallel to the vertical axis of the protractor, and
- 2.
- the uncocked gun axis points along the axis of the cylindrical
bob. (You may need to adjust the lengths of the supporting strings.)
SUGGESTED PROCEDURE:

![\framebox [5.2in]{\parbox[b]{5in}{\smallskip {\em PRECAUTIONS:}
Some spring gun...
...onsistent results be sure to recock the gun to the same stop.\smallskip \par }}](img122.gif)
*.3in
Find m and M by weighing on the single pan balance.
Find the height h
by measuring angle 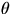 and the length L of the
pendulum.
and the length L of the
pendulum.
NOTE:  and L is not the length of the
string, (see Fig. 2).
and L is not the length of the
string, (see Fig. 2).
Suggestions on finding  : Find an approximate
: Find an approximate 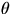 , and
then make a masking tape slit on
the back of the protractor at this approximate
, and
then make a masking tape slit on
the back of the protractor at this approximate 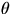 so your eye can
locate the proper viewing area to find a more accurate
so your eye can
locate the proper viewing area to find a more accurate 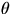 on subsequent firings. To avoid parallax (see appendix 4)
in reading the protractor choose a line of sight determined by the string in
front of the protractor and the string in back of the protractor. Careful
observation after a little practice will enable you to get
on subsequent firings. To avoid parallax (see appendix 4)
in reading the protractor choose a line of sight determined by the string in
front of the protractor and the string in back of the protractor. Careful
observation after a little practice will enable you to get 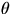 to within a
degree.
Calculate the initial velocity V of the combined pendulum bob and ball.
Calculate the initial velocity of the ball, u, as it leaves the gun.
Estimate the uncertainty in u.
[Hint: Since the largest uncertainty
is likely
to within a
degree.
Calculate the initial velocity V of the combined pendulum bob and ball.
Calculate the initial velocity of the ball, u, as it leaves the gun.
Estimate the uncertainty in u.
[Hint: Since the largest uncertainty
is likely 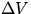 , then
, then 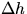 is important.
While h is a function of the measured L and
is important.
While h is a function of the measured L and 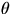 ,
the uncertainty in the angle measurement,
,
the uncertainty in the angle measurement, 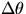 , will
probably dominate. To manually calculate the uncertainty in the resulting
trigonometric function, sometimes it is simpler to calculate separately the
function for
, will
probably dominate. To manually calculate the uncertainty in the resulting
trigonometric function, sometimes it is simpler to calculate separately the
function for 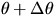 and for
and for 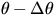 .
Otherwise the smart form can do this for you.
Remember that errors propagate
when one adds or subtracts by using the absolute not the relative errors.]
.
Otherwise the smart form can do this for you.
Remember that errors propagate
when one adds or subtracts by using the absolute not the relative errors.]
|
|
|

|
PART II. RANGE MEASUREMENTS
HORIZONTAL SHOT:
*.3in
After finding u, (the velocity of the ball leaving the
gun) predict the impact point on the floor for the
ball when shot horizontally from a position on the table.
To check your prediction experimentally:
*.3in
- (i)
- Use the plumb bob to check that the initial velocity is horizontal.
- (ii)
- Measure
all distances from where the ball starts free fall (not
from the cocked position). All measurements of course refer to the bottom of
the ball so x = 0 corresponds to the radius of the ball beyond the end of
the gun rod. Check that the gun's recoil does not change x.
- (iii)
- Fasten (with masking tape) a piece of computer paper at the
calculated point of impact, and just beyond the paper place a box
to catch the ball on the first bounce.
- (iv)
- Record results of several shots. (The ball's impact on the paper leaves
a visible mark.) Estimate the uncertainty in the observed range.
- (v)
- Is the observed range (including uncertainty) within that predicted.
Work backwards from the observed range to calculate the initial
velocity u. This u is
probably more accurate than the value obtained with the ballistic pendulum.
ELEVATED SHOT:
*.3in
Use the stand provided to elevate the gun at an
angle above the horizontal. The plumb bob will give the angle of
elevation, e.g. 90o - protractor reading.
For the elevated gun, be sure to include the additional initial
height above the floor of the uncocked ball.
Before actually trying a shot at an angle, again predict the range but
use the
value of u which you found from the horizontal shot. (See item 3 above).
Make several shots, record the results and compare with predictions.
QUESTION:
From the measured values of u and V calculate the kinetic
energy of the ball before impact, 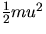 and the ball and
pendulum together after impact,
and the ball and
pendulum together after impact, 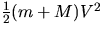 .What became of the difference?
.What became of the difference?
OPTIONAL:
*.3in

2. Find the spring constant k of the gun from
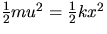 .
.




Next: M-6 Uniform Circular Motion
Up: PHYS 201/202 and 207/208
Previous: M-4 Acceleration in Free Fall
Michael Winokur
4/7/2000
![\begin{figure}
\centering
\includegraphics [height=2.70in]{figs/l103/m05-3.eps}...
...
\centering
\includegraphics [height=1.70in]{figs/l103/m05-r4.eps}
\end{figure}](img120.gif)

![\framebox [5.2in]{\parbox[b]{5in}{\smallskip {\em PRECAUTIONS:}
Some spring gun...
...onsistent results be sure to recock the gun to the same stop.\smallskip \par }}](img122.gif)

![\begin{figure}
\centering
\includegraphics [height=2.3in]{figs/l103/m05-6.eps}
\end{figure}](img130.gif)
![]() and the ball and
pendulum together after impact,
and the ball and
pendulum together after impact, ![]() .What became of the difference?
.What became of the difference? 