



Next: MC-7 Simple Pendulum
Up: PHYS 201/202 and 207/208
Previous: M-5 Projectile Motion
OBJECT: To verify experimentally that the centripetal force, Fc is
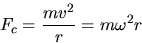
APPARATUS:
Fig. 1 is a schematic of the equipment. The bobs and
springs are removable for weighing. Not shown are table clamp and pulley,
slotted masses and weight hanger.
Figure 1:
The UCM apparatus.
![\begin{figure}
\centering
\includegraphics [height=4in]{figs/l103/m06-1.eps}
\end{figure}](img136.gif) |
INTRODUCTION:
A variable speed motor drives the rotating system which
has two slotted bobs which slide on a low friction bar. One
adjusts the speed until one bob just covers the optical light pipe and thus
reduces the signal seen at the center of the rotating system to zero.
A revolutions counter is on the shaft.
The counter operates by sensing the rotating magnetic poles and
electronically reads out
directly the frequency of revolution in rpm.
A spring (plus any friction) supplies the centripetal
force required to keep the bob
traveling in a circle.
If one measures first the frequency of rotation required
to make the bob just cover the optical light pipe,
and if one then measures the force required to pull the bob out the same
distance when the system is not rotating, one can check whether
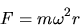
where r is the distance from the axis of rotations to the center of mass
of the bob.
Pre-lab Quiz
You should be able to complete this brief quiz before proceding.
SUGGESTIONS:
- 1.
- Find the mass of the nickel plated brass bob; also the
aluminum bob.
- 2.
- Dynamic measurement of the force: Attach the brass bob to
the spring. Replace the lucite cover, and adjust the motor speed until the
light from the light pipe at the center of the rotating system goes to zero.
Record the rotation frequency.
To correct for frictional effects of the bob on the bar, record the
frequencies both as the speed is increasing to the correct value and and
as the speed is decreasing from too high a value. Since the direction of
the frictional force reverses for the two cases, the average should eliminate
the frictional effect.
Repeat several times so you can estimate the
average or standard deviation of your values.
- 3.
- Static measurement of the force: Use the string, pulley and weight
holder plus slotted weights to measure the force required to stretch the spring
so that the optical light pipe is again just covered. Devise a way to avoid
error caused by the friction at the pulley and of the sliding bob on the bar.
- 4.
- While the spring is stretched in item 3 to its proper length, measure the
distance r from the axis of rotation to the center of mass of the bob. The
c. of m. of the bob is marked on it.
Figure 2:
Static measurement of the force using hanging weights
![\begin{figure}
\centering
\includegraphics [height=3.5in]{figs/l103/m06-2.eps}
\end{figure}](img138.gif) |
- 5.
- Compare the force as computed from
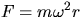 and as measured by
stretching the spring.
In computing the centripetal force, also take into consideration the mass
of the spring. One
can show (Weinstock, American Journal of Physics, 32,p. 370, 1964)
that
and as measured by
stretching the spring.
In computing the centripetal force, also take into consideration the mass
of the spring. One
can show (Weinstock, American Journal of Physics, 32,p. 370, 1964)
that  of the spring mass should be
added to the mass of the bob to obtain the total effective mass.
of the spring mass should be
added to the mass of the bob to obtain the total effective mass.
- 6.
- Repeat the above item 1 through item 5 but for the aluminum bob.
|
|
|

|
QUESTIONS:
- 1.
- Estimate the reliability of your measurements. How well do the
measured and computed forces agree? Try to account for any discrepancy.
- 2.
- How would the experiment be affected if gravitational and inertial mass
were not equal? [Gravitational mass refers to that appropriate for
Newton's principle of universal gravitation (
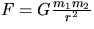 )
while inertial mass refers to the mass appropriate for Newton's second law
(F=ma).]
)
while inertial mass refers to the mass appropriate for Newton's second law
(F=ma).]




Next: MC-7 Simple Pendulum
Up: PHYS 201/202 and 207/208
Previous: M-5 Projectile Motion
Michael Winokur
4/7/2000
![]()
![]()
