



Next: M-5 Projectile Motion
Up: PHYS 201/202 and 207/208
Previous: M-3 Static Forces and Moments
OBJECTIVE: To measure ``g'', the acceleration of gravity.
APPARATUS:
*.3in
Free fall equipment: cylindrical bobs (identical except in
mass) which attach to
paper tape for recording spark positions; spark timer giving
sparks every 1/60 s; cushion; non-streamline bobs to study air resistance
(by adding a front plate).
INTRODUCTION:
*.3in
As shown in figure below the spark timer causes sparks to
jump from sharp point A (flush with the convex delrin surface)
through the falling vertical paper tape to the opposite sharp
point B flush with the other
convex delrin surface. As the bob (plus paper tape) undergoes free fall,
sparks from A to B mark the paper tape's position every 1/60 s. These
data give the bob's acceleration in free fall:
``g'', if air resistance be negligible.
See later for checking air resistance effects.
EXPERIMENTAL SUGGESTIONS:
- 1.
- Position spark timer chassis near table edge and
with the convex surfaces (A and B) extended beyond table edge.
Put cushion on floor directly under A and B.
- 2.
- Select the heaviest bob (no front plate).
Insert one end of about a meter of
paper tape between the two
halves of the cylindrical bob and fasten together with thumb screw.
- 3.
- Insert paper tape between A and B.
Hold the tape end
high enough (vertically) above A and B that the bob just touches
below A and B (and is centered). Start the spark and
immediately release tape plus bob. Discard any part of tape which fell
through the spark gap after bob hit the cushion.
![\begin{figure}
\ \
\includegraphics [width=2.55in]{figs/l103/m04-3.eps}
\end{figure}](img97.gif)
*.3in
[4.] Fasten sparked tape to table top with
masking tape. Place a meter stick on its side (on top of tape) so that
ends of the mm graduations touch the dot track on the tape; this
avoids parallax error: appendix 4.
[5.] Ignore the first spark dot; then mark and measure the
position of every other of the first 24 dots,
thus using 1/30 s as the time interval
instead of 1/60 s.
Estimate dot positions to 0.1 mm.
Don't move meter stick between readings!
Tabulate as in sample below.
[6.] Check the measurement set by remeasuring the tape
after moving the meter stick so
that the recorded dot positions will be different. The
differences should be the same. How close are they?
COMPUTER GENERATED TABULAR FORM FOR DATA:
| Spark | Real | Position of | Average | Average |
|
interval | time | every 2nd | velocity | acceleration |
| | spark (dot) | | |
|
i | t(i) | 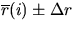 | 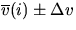 | 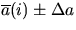 |
|
Units | sec | mm or cm |  |  |
| Errors | | 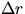 |  | 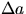 |
| 0 | t(0) | a | -- | -- |
|
1 | t(1) | b | b-a | (c-b)-(b-a) |
|
2 | t(2) | c | c-b | (d-c)-(c-b) |
|
3 | t(3) | d | d-c | (e-d)-(d-c) |
|
4 | t(4) | e | e-d | (f-e)-(e-d) |
|
5 | t(5) | f | f-e | (g-f)-(f-e) |
|
6 | t(6) | g | g-f | (h-g)-(g-f) |
|
7 | t(7) | h | h-g | (i-h)-(h-g) |
|
8 | t(8) | i | i-h | (j-i)-(i-h) |
|
9 | t(9) | j | j-i | (k-j)-(j-i) |
|
10 | t(10) | k | k-j | (l-k)-(k-j) |
|
11 | t(11) | l | l-k | (m-l)-(l-k) |
 | 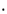 | 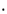 | 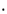 | 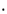 |
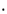 | 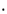 | 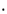 | 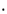 | 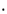 |
SUGGESTIONS ON HANDLING DATA:
*.3in
Let t = 0 be where your readings start. Tabulate the actual
readings, r, on the meter stick at the end of each time interval (as
in column 3 above); calculate the average velocity, 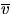 in each interval;
then calculate the average acceleration,
in each interval;
then calculate the average acceleration, 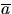 during each interval.
If you do the table by hand it may be easier to compute everything in
per time interval units and scale your answer when everything is done.
Find the average of the average
during each interval.
If you do the table by hand it may be easier to compute everything in
per time interval units and scale your answer when everything is done.
Find the average of the average 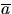 in each interval and convert (if necessary).
This average of the average
in each interval and convert (if necessary).
This average of the average 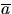 , namely ``
, namely ``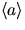 ''
is much more
accurate than fluctuations in the
''
is much more
accurate than fluctuations in the 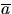 column might indicate.
Explain why. (Hint: Are the values independent? See last part, Suggestion
4) below.
With 1/30 s as the time interval,
plot ``r'' vs time,
column might indicate.
Explain why. (Hint: Are the values independent? See last part, Suggestion
4) below.
With 1/30 s as the time interval,
plot ``r'' vs time, 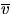 vs time, and
vs time, and 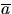 vs time.
Note that for
vs time.
Note that for 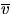 this value is the average v between to adjacent rows, i and i+1,
and therefore equals the instantaneous v at the middle of the
interval.
Use the slope of the velocity curve to find acceleration. Your can do
this by hand but graphical analysis tools should be available. This
approach is a better way of using all the data than the above
numerical one since averaging the
this value is the average v between to adjacent rows, i and i+1,
and therefore equals the instantaneous v at the middle of the
interval.
Use the slope of the velocity curve to find acceleration. Your can do
this by hand but graphical analysis tools should be available. This
approach is a better way of using all the data than the above
numerical one since averaging the 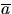 column involves
summing the
column involves
summing the 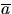 column and in such a sum all readings except
(b-a) and (m-l) drop out!
column and in such a sum all readings except
(b-a) and (m-l) drop out!
ERROR ANALYSIS:
*.3in
If readings a, b, c, etc.,
are good to 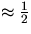 mm because of irregularity in the spark path,
the worst case would be for (b-a) to be in error by 1 mm. Since
these two measurements are to first order, uncorrelated, the errors should
add in quadrature
[see section on Errors]. Using every v(i) for your slope
determination is problematic because each v(i) and v(i+1) is
correlated [
mm because of irregularity in the spark path,
the worst case would be for (b-a) to be in error by 1 mm. Since
these two measurements are to first order, uncorrelated, the errors should
add in quadrature
[see section on Errors]. Using every v(i) for your slope
determination is problematic because each v(i) and v(i+1) is
correlated [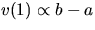 and
and 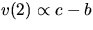 ]. Thus a linear-fit
of slope suffers from the same shortcoming as the average of the average
acceleration calculation noted in Suggestion 4!
Calculate the slope using only every other v(i). Does your new value for
``g'' vary much? Estimate the uncertainty in the slope.
Spark timing errors
are negligible. Air
resistance is a systematic error, small for the streamline bobs
at low velocities, but see the optional experiment below.
]. Thus a linear-fit
of slope suffers from the same shortcoming as the average of the average
acceleration calculation noted in Suggestion 4!
Calculate the slope using only every other v(i). Does your new value for
``g'' vary much? Estimate the uncertainty in the slope.
Spark timing errors
are negligible. Air
resistance is a systematic error, small for the streamline bobs
at low velocities, but see the optional experiment below.
EQUIVALENCE OF GRAVITATIONAL AND INERTIAL MASS:
*.3in
Galileo showed (crudely) that the acceleration of falling bodies
was independent of the mass. Use the light plastic bob (identical in size
and shape to the massive bob) to
repeat the free fall experiment and thus check
quantitatively this equivalence (when air resistance effects are small
enough). If you are planning to do the optional experiment which follows,
you should skip this part.
--------------------------
LOCAL VALUE OF g:
The UW Geophysics Department determined `` g '' accurately
for room 4300 Sterling Hall. A plaque on the northwest window sill gives
g = 9.803636 + 0.000001 m/s2.
--------------------------
QUESTION: Do your value(s) of `` g '' agree within your assigned
errors?
OPTIONAL EXPERIMENTS
*.3in
[A.] EFFECT OF AIR RESISTANCE: While air effects are small for
streamlined objects at low velocities, they can become large,
e.g. on a parachute.
To observe and correct for them,
first make the bobs non-streamline by inserting into the bottom of the
bob the banana plug holding a small flat plate. Then
repeat the experiment for the
non-streamline bobs (front plate attached), identical except for mass.
There are four possible mass combinations.
Since the force of air resistance, f(v), is
a function of only velocity if the size, shape and roughness are the
same, then f(v) on the two bobs will be almost
the same since their velocities are similar. The net force on the
falling body is then F=mg-f(v). Hence
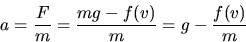
and
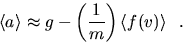
Thus if we measure 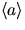 for bobs identical except in mass and
plot
for bobs identical except in mass and
plot 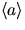 against 1/m, we should obtain a straight line whose
extrapolation to (1/m) = 0 should give g. To further test the validity
of this hypothesis you should plot the same data as recorded by other
lab groups on your plot. If the data permits a simple linear fit
you should be able extrapolate to infinite mass (i.e. the y-intercept).
against 1/m, we should obtain a straight line whose
extrapolation to (1/m) = 0 should give g. To further test the validity
of this hypothesis you should plot the same data as recorded by other
lab groups on your plot. If the data permits a simple linear fit
you should be able extrapolate to infinite mass (i.e. the y-intercept).
*.3in
[B.] MEASUREMENT OF REACTION TIME BY FREE FALL:
- (1)
- With thumb and forefinger
grasp a vertical meter stick at the 50 cm mark. Release and grab
it again as quickly as possible. From the distance
through which the 50 cm mark fell, calculate the time of free fall of the
meter stick. This time is your total reaction time involved in
releasing and grasping again.
- (2)
- Have your partner hold the vertical meter stick while you place your
thumb and forefinger opposite the 50 cm mark but not grasping it. When
your partner releases the stick, grab it as soon as possible. Again from
the distance through which the 50 cm mark fell, calculate the time of free
fall of the meter stick. Compare this time with the other method.
Why may these reaction times be different?
OPTIONAL QUESTIONS:
- 1.
- Estimate the effect on your ``g" value
of the air's buoyant force, Fa for air density,
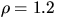 kg/m3
and brass bob density,
kg/m3
and brass bob density, 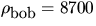 kg/m3.
kg/m3.
Hint:
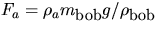 (why?), and
(why?), and
![$a =g[1-(\rho_{a}/\rho_{\mbox{\small bob}})]$](img117.gif) (why?).
(why?).
- 2.
- According to universal gravitation, the moon also accelerates the bob
with a value am of
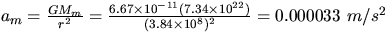
where G is the constant of universal gravitation, Mm is the mass of the
moon, and r is the distance between the moon and the bob.
Since this am
is 33 times the uncertainty quoted for the local g value,
why doesn't the plaque also indicate the position of the moon at the time of
measurement?
Hint: Remember the acceleration g in an
orbiting earth satellite provides the centripetal acceleration for the
circular motion but does not appear as ``weight" of an object in the
satellite. While to first order the moon and sun effects are negligible,
there are detectable tidal effects in the earth  which one
corrects for in the absolute measurements. See Handbuch der Physics, Vol
XLVIII, p. 811; also Wollard and Rose, ``International Gravity
Measurements", UW Geophysical and Polar Research Center, (1963) p. 183. On
pages 211 and 236, they also describe the accurate absolute g determination
with two quartz pendula in room 70 Science Hall from which the plaque value
in Room 4300 Sterling derives.
which one
corrects for in the absolute measurements. See Handbuch der Physics, Vol
XLVIII, p. 811; also Wollard and Rose, ``International Gravity
Measurements", UW Geophysical and Polar Research Center, (1963) p. 183. On
pages 211 and 236, they also describe the accurate absolute g determination
with two quartz pendula in room 70 Science Hall from which the plaque value
in Room 4300 Sterling derives.




Next: M-5 Projectile Motion
Up: PHYS 201/202 and 207/208
Previous: M-3 Static Forces and Moments
Michael Winokur
4/7/2000
![\begin{figure}
\ \
\includegraphics [width=2.55in]{figs/l103/m04-3.eps}
\end{figure}](img97.gif)

![]()
![]()
![]()
![]() which one
corrects for in the absolute measurements. See Handbuch der Physics, Vol
XLVIII, p. 811; also Wollard and Rose, ``International Gravity
Measurements", UW Geophysical and Polar Research Center, (1963) p. 183. On
pages 211 and 236, they also describe the accurate absolute g determination
with two quartz pendula in room 70 Science Hall from which the plaque value
in Room 4300 Sterling derives.
which one
corrects for in the absolute measurements. See Handbuch der Physics, Vol
XLVIII, p. 811; also Wollard and Rose, ``International Gravity
Measurements", UW Geophysical and Polar Research Center, (1963) p. 183. On
pages 211 and 236, they also describe the accurate absolute g determination
with two quartz pendula in room 70 Science Hall from which the plaque value
in Room 4300 Sterling derives.