



Next: M-4 Acceleration in Free Fall
Up: PHYS 201/202 and 207/208
Previous: M-2 Equilibrium of Forces
OBJECTIVE:
To check experimentally the conditions for equilibrium of a rigid body.
APPARATUS:
*.3in
Model of rigid derrick, slotted masses and weight hangers,
knife edge (mounted in wall bracket), vernier caliper, single pan balance.
INTRODUCTION:
*.3in
Equilibrium requires that the
net linear acceleration and the net angular acceleration be zero.
Hence 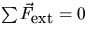 and
and 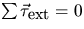 .
We treat the rigid derrick as a two dimensional structure
so the vector equations become:
.
We treat the rigid derrick as a two dimensional structure
so the vector equations become:
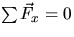 ,
, 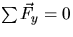 and
and 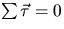 .
The choice of the perpendicular axis about which one computes torques is
arbitrary so in part 4 below we choose an axis which simplifies
calculations.
.
The choice of the perpendicular axis about which one computes torques is
arbitrary so in part 4 below we choose an axis which simplifies
calculations.
Pre-lab Quiz
SUGGESTED PROCEDURES:
- 1.
- Place a load of about 2 kg for m2.
- 2.
- Determine experimentally the force m3 to hold
the derrick in
equilibrium with the top member level. Since this is
an unstable equilibrium,
adjust m3 so that the derrick will fall either way
when displaced equally from equilibrium.
To find the uncertainty in m3 increase
or decrease m3 until you know the smallest force m3
which is definitely too large and the largest which
is definitely too small.
![\begin{figure}
\includegraphics [width=2.8in]{figs/l103/m03-6.eps}
\end{figure}](img94.gif)
*.3in
[3.] Weigh the derrick (use single pan balance) and find the
horizontal distance between the center of the stirrup and the vertical line
through the center of gravity (c.g.) of the derrick. (Use the knife edge
mounted in a wall bracket for locating the c.g.)
[4.] Calculate how accurately the 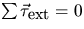 condition is
satisfied about the point where the lower stirrup supports the derrick.
Note: distance from rotation axis must include stirrup axle radius
(use vernier caliper).
[5.]
Calculate the force
condition is
satisfied about the point where the lower stirrup supports the derrick.
Note: distance from rotation axis must include stirrup axle radius
(use vernier caliper).
[5.]
Calculate the force 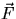 exerted by the stirrup on the derrick.
[6.]
Choose an axis that is not on the line of action of any force and
calculate how closely
is satisfied about that axis. Is the discrepancy reasonable?
Make your answer as quantitative as you can.
(Include the uncertainty in
exerted by the stirrup on the derrick.
[6.]
Choose an axis that is not on the line of action of any force and
calculate how closely
is satisfied about that axis. Is the discrepancy reasonable?
Make your answer as quantitative as you can.
(Include the uncertainty in 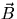 and any other measurements).
and any other measurements).




Next: M-4 Acceleration in Free Fall
Up: PHYS 201/202 and 207/208
Previous: M-2 Equilibrium of Forces
Michael Winokur
4/7/2000
![\begin{figure}
\includegraphics [width=2.8in]{figs/l103/m03-6.eps}
\end{figure}](img94.gif)
![\begin{figure}
\includegraphics [width=2.8in]{figs/l103/m03-6.eps}
\end{figure}](img94.gif)
