Errors and Uncertainties

  Reliability estimates of measurements greatly enhance their value. Thus, saying that the average diameter of a cylinder is $10.00\pm 0.02\ mm$ tells much more than the statement that the cylinder is a centimeter in diameter.

To physicists the term ``error" is interchangeable with `` uncertainty" and does not have the same meaning as ``mistake". Mistakes, such as ``errors" in calculations, should be corrected before estimating the experimental error. In estimating the reliability of a single quantity (such as the diameter of a cylinder) we recognize several different kinds and sources of error:

FIRST, are actual variations of the quantity being measured, e.g. the diameter of a cylinder may actually be different in different places. You must then specify where the measurement was made; or if one wants the diameter in order to calculate the volume, first find the average diameter by means of a number of measurements at carefully selected places. Then the scatter of the measurements will give a first estimate of the reliability of the average diameter.

SECOND, the micrometer caliper used may itself be in error. The errors thus introduced will of course not lie equally on both sides of the true value so that averaging a large number of readings is no help. To eliminate (or at least reduce) such errors, we calibrate the measuring instrument: in the case of the micrometer caliper by taking the zero error (the reading when the jaws are closed) and the readings on selected precision gauges of dimensions approximately equal to those of the cylinder to be measured. We call such errors systematic.

THIRD, Another type of systematic error can occur in the measurement of a cylinder: The micrometer will always measure the largest diameter between its jaws; hence if there are small bumps or depressions on the cylinder, the average of a large number of measurements will not give the true average diameter but a quantity somewhat larger. (This error can of course be reduced by making the jaws of the caliper smaller in cross section.)

FINALLY, if one measures something of definite size with a calibrated instrument, errors of measurement still exist which (one hopes) are as often positive as negative and hence will average out in a large number of trials. For example, the reading of the micrometer caliper may vary because one can't close it with the same force every time. Also the observer's estimate of the fraction of the smallest division varies from trial to trial. Hence the average of a number of these measurements should be closer to the true value than any one measurement. Also the deviations of the individual measurements from the average give an indication of the reliability of that average value.

Average Deviation:

If one finds the average of the absolute values of the deviations, this ``average deviation from the mean" may serve as a measure of reliability. For example, let column 1 represent 10 readings of the diameter of a cylinder taken at one place so that variations in the cylinder do not come into consideration, then column 2 gives the magnitude (absolute) of each reading's deviation from the mean.

Measurements Deviation from Ave.

      9.943 mm 0.000

9.942 0.001

9.944 0.001

9.941 0.002

9.943 0.000

9.943 0.000

9.945 0.002 Diameter =

9.943 0.000

$$\pm$$ 9.941 0.002

$$\underline{~9.942~} \underline{~0.001~}$$

$$\rightarrow \sim$$ Ave = 9.943 mm    

Expressed algebraically, the average deviation from the mean is $= (\sum \vert x_i-\bar{x}\vert)/n$ where x_i is the i^th measurement of n taken, and $\bar x$ is the mean or arithmetic average of the readings.

Standard Deviation:

  A more useful measure of the spread in a set of measurements is the standard deviation S (or root mean square deviation). One defines S as

$$S=\sqrt{\frac{1}{n}\sum_{i=1}^{n}(x_{i}-\overline{x})^{2}}$$

where $\overline{x}$ is the mean or arithmetical average of the set of n measurements and x_i is the i^th measurement.

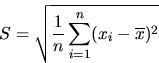
The standard deviation, S, clearly weights large deviations more heavily than the average deviation and thus gives a less optimistic estimate of the reliability. Careful analysis shows that even a better estimator (and appreciably less optimistic for small sets of measurements) is

$$\sigma \sim \sqrt{n/(n-1)} ~S~ = ~\sqrt{\frac{\sum (x_i-\bar{x})^2}{n-1}}$$

This estimator, $\sigma$, is the ``universe" or ``parent" standard deviation; its square, $\sigma^{2}$ the variance. (For an explanation of the $\sqrt{n(n-1)}$ factor see Parratt, ``Probability and Experimental Errors in Science", Wiley & Sons, 1961, p. 89f).

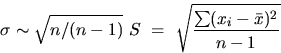
If the error distribution is ``normal" (i.e. the errors, $\epsilon$ have a Gaussian distribution, $e^{-\epsilon^{2}}$, about zero), then on average 68% of a large number of measurements will lie closer than $\sigma$ to the true value. While few measurement sets have precisely a ``normal" distribution, the main differences tend to be in the tails of the distributions. If the set of trial measurements are generally bell shaped in the central regions, the ``normal" approximation generally suffices.

Relative error and percentage error:
Let $\epsilon$ be the error in a measurement whose value is a. Then $(\frac{\epsilon}{a})$ is the relative error of the measurement, and $100\ (\frac{\epsilon}{a})\%$ is the percentage error. These terms are useful in laboratory work.

SYSTEMATIC ERRORS IN THE LABORATORY STANDARDS OF
LENGTH, TIME AND MASS

  For the experiments in this manual these systematic errors are usually negligible compared to other uncertainties. An exception sometimes occurs for the larger masses especially the 100 gram, the 500 gram, and 1 kg masses. Some contain drilled holes into which lead shot and a plug have been added to adjust the mass to within tolerance (typically $1.000\pm 0.003$ kg). Occasionally a plug works loose and the calibration lead shot is lost. You can check the assigned mass values by weighing them on the triple beam balances. Report any deviations greater than 0.4% to the instructor.

UNCERTAINTY ESTIMATE FOR A RESULT INVOLVING MEASUREMENTS OF
SEVERAL INDEPENDENT QUANTITIES

  A.) If the desired result is the sum or difference of two measurements, the ABSOLUTE uncertainties ADD:
Let $\Delta x$ and $\Delta y$ be the errors in x and y respectively. For the sum we have $z=x+\Delta x + y + \Delta y = x + y + \Delta x + \Delta y$and the relative error is $\frac{\Delta x + \Delta y}{x + y}$. Since the signs of $\Delta x$ and $\Delta y$can be opposite, adding the absolute values gives a pessimistic estimate of the uncertainty. If errors have a normal or Gaussian distribution and are independent, they combine in quadrature, i.e. the square root of the sum of the squares, i.e.,

$$\Delta z=\sqrt{\Delta x^{2}+\Delta y^{2}}$$

For the difference of two measurements we obtain a relative error of $\frac{\Delta x - \Delta y}{x - y}$. which becomes very large if x is nearly equal to y. Hence avoid, if possible, designing an experiment where one measures two large quantities and takes their difference to obtain the desired quantity.

B.) If the desired result involves multiplying (or dividing) measured quantities, then the RELATIVE uncertainty of the result is the SUM of the RELATIVE errors in each of the measured quantities.

Proof:

$$\mbox{Let}~~~ z =\frac{x_1~x_2~x_3 .....}{y_1~y_2~y_3 .....}~~~ \mbox{and hence} \hspace*{2.1in}$$

$$\ln{z} =\ln{x_1} +\ln{x_2} +\ln{x_3} + ..... -\ln{y_1} -\ln{y_2} -\ln{y_3} - .....$$

Then find the differential, $d(\ln{z)}$:

$$d(\ln{z}) =\frac{dz}{z} =\frac{dx_1}{x_1}+\frac{dx_2}{x_2}+\... ... -\frac{dy_1}{y_1}+\frac{dy_2}{y_2}+\frac{dy_3}{y_3} - .....$$

Consider finite differentials, $\Delta z$, etc. and note that the most pessimistic case corresponds to adding the absolute value of each term since $\Delta x_{i}$ and $\Delta y_{i}$ can be of either sign. Thus

$$\frac{\Delta z}{z}=\sum_{i}(\frac{\Delta x}{x})+\sum_{i}(\frac{\Delta y}{y})$$

Again, if the measurement errors are independent and have a Gaussian distribution, the relative errors will add in quadrature:

$$\frac{\Delta z}{z}= \sqrt{\sum_{i}(\frac{\Delta x}{x})^{2}+\sum_{i}(\frac{\Delta y}{y})^{2}}$$

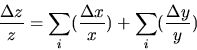
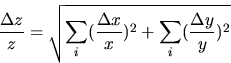
C.) Corollary: If the desired result is a POWER of the measured quantity, the RELATIVE ERROR in the result is the relative error in the measured quantity MULTIPLIED by the POWER: Thus z = xⁿ and

$$\frac{\Delta z}{z} = n \frac{\Delta x}{x}.$$

The above results also follow in more general form: Let R = f(x,y,z) be the functional relationship between three measurements and the desired result. If one differentiates R, then

$$dR = \frac{\partial{f}}{\partial{x}} dx + \frac{\partial{f}}{\partial{y}} dy + \frac{\partial{f}}{\partial{z}} dz$$

gives the uncertainty in R when the uncertainties dx, dy and dz are known.

For example, consider the density of a solid (Exp. M1). The relation is

$$\rho~= ~\frac{m}{\pi r^2 L}$$

where m = mass, r = radius, L = length, are the three measured quantities and $\rho$ = density. Hence

$$\frac{\partial{\rho}}{\partial{m}}=\frac{1}{\pi r^2L} ~~~~~~... ...~~~~~ \frac{\partial{\rho}}{\partial{L}}=\frac{-m}{\pi r^2L^2}$$

and so

$$d\rho=\frac{1}{\pi r^2L} ~dm +~\frac{-2m}{\pi r^3L} ~dr +~ \frac{-m}{\pi r^2L^2}~ dL.$$

To get the relative error divide by $\rho=m/\pi r^2 L$. The result, if one drops the negative signs, is

$$\frac{d\rho}{\rho} = \frac{dm}{m} + 2 \frac{dr}{r} + \frac{dL}{L}$$

and represents a worst possible combination of errors. For small increments:

$$\frac{\Delta\rho}{\rho} = \frac{\Delta m}{m} + 2 \frac{\Delta r}{r} + \frac{\Delta L}{L}$$

and

$$\Delta\rho = \rho \left[ \frac{\Delta m}{m} + 2 \frac{\Delta r}{r} + \frac{\Delta L}{L} \right]$$

Again if the errors have normal distribution, then

$$\frac{\Delta\rho}{\rho} = \sqrt{\left(\frac{\Delta m}{m}\rig... ...rac{\Delta r}{r}\right)^2 + \left(\frac{\Delta L}{L}\right)^2}$$

SIGNIFICANT FIGURES

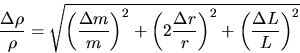
Suppose you have measured the diameter of a circular disc and wish to compute its area $A=\pi d^{2}/{4}=\pi r^{2}$. Let the average value of the diameter be $24.326\pm 0.003$ mm ; dividing d by 2 to get r we obtain $12.163\pm 0.0015$ mm with a relative error $\frac{\Delta r}{r}$ of $\frac{0.0015}{12}=0.00012$. Squaring r we have

The relative error in r² is twice that in r; hence r² is uncertain to about 4 in the 5$^{\mbox{\small th}}$ digit since $2\frac{\Delta r}{r} \times r^2$ is $0.00024\times 147.94=0.0355\approx 0.04$.Thus $r^{2}=147.94\pm 0.04$ mm². There is clearly no point in carrying figures beyond the 5$^{\mbox{\small th}}$ in further calculation. Hence for this example the first five figures are called significant. Now in computing the area $A = \pi r^{2}$ how many digits of $\pi$ must be used? A pocket calculator with $\pi=3.141592654$ gives

$$A = \pi r^{2}= \pi\times 147.94 = 464.7672172 \mbox{ mm}^{2}$$

However $\frac{\Delta A}{A}=2\frac{\Delta r}{r}=0.00024.$Our answer should then be written as $A=464.77\pm 0.11$ m². Note that the same answer results from $\pi=3.1416$, but that $\pi=3.142$ gives $A=464.83\pm 0.11$ mm² which differs from the correct value by 0.06 mm², an amount comparable to the estimated uncertainty.

A rule of rather general applicability is to use one more digit in constants than is available in your measurements, and to save not more than one more digit in computations than the number of significant figures in the data. When using a calculator, one can include many more digits in the calculations.
However, at the end be sure to round off the final answer to display the correct number of significant figures.

SAMPLE QUESTIONS

1.

How many significant figures are there in the following number?

(a)

976.45

(b)

4.000

(c)

10

2.

Round off each of the following numbers to three significant figures.

(a)

4.455

(b)

4.6675

(c)

2.045

3.

A function has the relationship Z(A,B)=A+B³ where A and B are found to have uncertainties of $\pm \Delta A$ and $\pm \Delta B$ respectively. Find $\Delta Z$ in term of A, B and the respective uncertainties assuming the errors are uncorrelated.

4.

What happens to $\sigma$, the standard deviation, as you make more and more measurements? what happens to $\overline{\sigma}$, the standard deviation of the mean?

(a)

They both remain same

(b)

They both decrease

(c)

$\sigma$ increases and $\overline{\sigma}$ decreases

(d)

$\sigma$ approachs a constant and $\overline{\sigma}$ decreases

Working Demo

The htmlscript Quiz System working demo is now available.

• Quiz System Working Demo

Suggestions on Form for Lab Notebooks:

NUMBER AND TITLE (e.g. E1. ELECTROSTATICS)

Date performed:____________                                Partner:_________________________

Subdivisions: If appropriate, name and number each section as in the manual.

DATA:
  Label numbers and give units. If appropriate, record the data in tabular form. Label the tables and give units.

CALCULATIONS:

  State the equations used and present a sample calculation. (Inclusion of the arithmetic is not necessary.)

CONCLUSIONS:

  If any important conclusions follow from the experiments, state them and show by a brief statement how they follow. Compare your results with accepted values if the experiment has involved the measurements of a physical constant.

Errors:

 Some of your experiments will be qualitative while others will involve quantitative measurements of physical constants. In experiments where it is appropriate, estimate the uncertainty of each measurement used in a calculation and compute the uncertainty of the result. Does your estimate of uncertainty indicate satisfactory agreement between your result and the accepted one (or between your several values if you have several)? Intelligent discussion is welcomed, but don't make this section a burden on you.