



Next: M-13 Gyroscope
Up: PHYS 201/202 and 207/208
Previous: M-11 Young's Modulus of
OBJECTIVES: To study a torsion pendulum and to measure a shear
modulus.
APPARATUS:
Wall mounted torsion pendulum
(large disk plus suspension assembly); rods
of different lengths, diameters and material;
a ring and two cylindrical masses; timer, tally counter.
INTRODUCTION:
If a torque 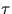 twists a rod, then the
angle
twists a rod, then the
angle 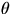 through which
the rod twists is proportional to the torque if the elastic limit is not
exceeded: Thus
through which
the rod twists is proportional to the torque if the elastic limit is not
exceeded: Thus 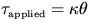 where
where 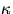 is the torsion constant.
is the torsion constant.
Figure 1:
(a) A thin-walled hollow cylinder. (b) The cylinder is twisted by
applying a torque. (c) The angle of shear 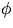 and the
angle of twist
and the
angle of twist 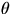 .
.
![\begin{figure}
\centering
\includegraphics [width=4.8in]{figs/m12-1.eps}
\end{figure}](img228.gif) |
The equal and opposite reaction torque is
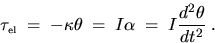
Since this is the same mathematical form as
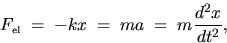
it has a similar solution: 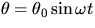 where
where
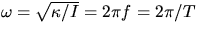 . Thus the system
undergoes angular simple harmonic motion, SHM, with
. Thus the system
undergoes angular simple harmonic motion, SHM, with
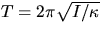 and T is independent of amplitude, (in contrast to a simple pendulum where
and T is independent of amplitude, (in contrast to a simple pendulum where
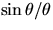 is only
is only 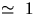 ). For simple
geometries, one readily calculates the rotational inertia I. Hence
measuring T can determine precisely the torsion constant,
). For simple
geometries, one readily calculates the rotational inertia I. Hence
measuring T can determine precisely the torsion constant, 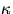 .To relate the torsion constant
.To relate the torsion constant 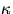 to the shear modulus Ms,
consider first
a tangential force dFt applied to the end of a thin (dr thick) hollow
tube. This tangential force/area is the shear
stress and equals
to the shear modulus Ms,
consider first
a tangential force dFt applied to the end of a thin (dr thick) hollow
tube. This tangential force/area is the shear
stress and equals 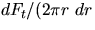 ). The resultant shear strain
is the angle [see Fig. 1(c)]
). The resultant shear strain
is the angle [see Fig. 1(c)]
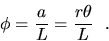
Multiplying the stress by r/r gives
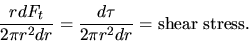
Hence the shear modulus Ms becomes:
![\begin{displaymath}
M_s = \frac{\mbox{shear stress}}{\mbox{shear
strain}} = \fr...
...frac{Ld \tau}{
\theta (2\pi r^3)dr} \hspace{.5in} \mbox{[tube]}\end{displaymath}](img239.gif)
and 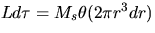 . If one integrates from 0 to R,
the tube then becomes a solid rod:
. If one integrates from 0 to R,
the tube then becomes a solid rod:
![\begin{displaymath}
L \tau = M_s \theta \; 2\pi \left( \frac{R^4}{4}\right)
\hspace{.5in} \mbox{[solid rod]}.\end{displaymath}](img241.gif)
Thus
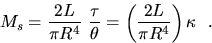
SUGGESTED EXPERIMENTS: (only one of which need be performed)
- 1.
- Determine the shear modulus of one or more materials by measuring
the period of a torsion pendulum with the materials as the suspension.
- 2.
- Use the result of Exp. 1 (or from a table of shear moduli)
to calculate the
period of a torsion pendulum with the ring (or the two cylindrical
masses) placed on the disc. Compare with the measured value of the period.
- 3.
- Check the expression for shear modulus,
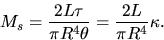
where 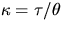 is the torsion constant, R and L are the
radius and length
of the rod,
is the torsion constant, R and L are the
radius and length
of the rod, 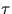 is the torque and
is the torque and 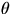 is the angular displacement.
Use rods of the same material but different lengths and diameters.
is the angular displacement.
Use rods of the same material but different lengths and diameters.
- 4.
- Determine how the period of the torsion pendulum depends on the length
and diameter of the rod; also on the rotational inertia of the suspended
mass. Check that the period is independent of angular amplitude (as long as
one is below the elastic limit). Compare with theory.
QUESTION:
Is it reasonable to ignore the rotational
inertia of the
suspending rod? Check your answer by estimating the ratio of the rod's
rotational inertia to that of the large disc.




Next: M-13 Gyroscope
Up: PHYS 201/202 and 207/208
Previous: M-11 Young's Modulus of
Michael Winokur
4/7/2000
![]() twists a rod, then the
angle
twists a rod, then the
angle ![]() through which
the rod twists is proportional to the torque if the elastic limit is not
exceeded: Thus
through which
the rod twists is proportional to the torque if the elastic limit is not
exceeded: Thus ![]() where
where ![]() is the torsion constant.
is the torsion constant.
![\begin{figure}
\centering
\includegraphics [width=4.8in]{figs/m12-1.eps}
\end{figure}](img228.gif)
![]()
![]()
![]()
![]()
![]()
![\begin{displaymath}
L \tau = M_s \theta \; 2\pi \left( \frac{R^4}{4}\right)
\hspace{.5in} \mbox{[solid rod]}.\end{displaymath}](img241.gif)
![]()
![]()