



Next: MC-14-Elastic and Inelastic Collisions
Up: PHYS 201/202 and 207/208
Previous: M-12 Torsion Pendulum and Shear
OBJECTIVE:
To study gyroscopes and to check the
relationship between angular momentum, applied torque and rate of
precession.
REFERENCES:
Don't do this experiment before reading about
angular momentum and gyroscopes; see also the Mitac
Instruction Manual, especially pages 1-7, experiments 1-4, pages
11-14, and Sec. 6 on ``Operation''.
APPARATUS: Mitac Gyroscope, 150 g and 300 g snap on
slotted masses, and stroboscope.
SUGGESTIONS:
- 1.
- Read the sections of the Mitac Manual referred to
above, start the gyroscope, and experiment with it. For example, predict the
direction of precession when a certain torque is applied; then check it
experimentally.
- 2.
- When you have become familiar with the operation of the
gyroscope perform
the following quantitative experiment:
![$\textstyle\parbox{5.3in}{
\item[i.] Calculate the rotor's angular momentum from the following data:}$](img245.gif)
|
Outer diameter of rotor | 20 | . | 0 | cm |
|
Inner diameter of rotor | 15 | . | 1 | cm |
|
Thickness of rotor | 2 | . | 54 | cm |
|
Rotor webb thickness | 0 | . | 435 | cm |
|
Hub diameter | 3 | . | 01 | cm |
|
Mass of rotor | 2 | . | 73 | kg |
|
Rotor rpm | 150 | . | | |
|
(Check rotor rpm with the stroboscope) | | . | | |
Figure 1:
(a) A thin-walled hollow cylinder. (b) The cylinder is twisted by
applying a torque. (c) The angle of shear 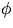 and the
angle of twist
and the
angle of twist 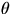 .
.
![$\textstyle\parbox{5.3in}{
\item[ii.] Place one of the supplied weights into the...
...you should make.
The experiments in the Mitac Manual are good possibilities. }$](img246.gif)
Alternative M-13 Gyroscope:
OBJECTIVE: To study gyroscopic effects especially precession and nutation.
APPARATUS: Air bearing gyroscope, torque weights, timer, stroboscope.
INTRODUCTION: Review gyroscope treatment in text (or in
handout).
CAUTION:
The air bearing surfaces and torque
shaft can easily suffer
damage so handle carefully: e.g. when the air pressure is on (and ball
friction negligible) the glued-on torque shaft may break off if
the shaft bangs against the stationary ball holder.
![\includegraphics [height=3.3in]{figs/m13-01.eps}](img248.gif)
SUGGESTED STUDIES:
- 1.
- Qualitative explorations: With air flow on to minimize friction,
spin ball by twisting the torque shaft with thumb and forefinger. Observe
precession about the vertical Z axis, and observe nutation
(torque shaft
bobbing
up and down) for different torque weights on the shaft and for different
spin angular velocities,
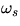 . Upon what factors does the precession
depend?
Observe the three basic nutation patterns when the total torque
weight, m, has:
. Upon what factors does the precession
depend?
Observe the three basic nutation patterns when the total torque
weight, m, has:
a) no initial vertical velocity:
| |
|
![\includegraphics [height=0.6in]{figs/m13-02.eps}](img250.gif)
|
b) a small initial vertical velocity:
| |
|
![\includegraphics [height=0.6in]{figs/m13-03.eps}](img251.gif)
|
c) an initial small horizontal velocity:
| |
|
![\includegraphics [height=0.6in]{figs/m13-04.eps}](img252.gif)
|
- 2.
- Measure the angular acceleration,
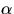 , from the air friction: For
low
, from the air friction: For
low 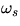 use a stopwatch and time the revolutions of a mark on the
rotating shaft. Plot spin angular velocity,
use a stopwatch and time the revolutions of a mark on the
rotating shaft. Plot spin angular velocity, 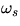 , versus time (remember to
plot average
, versus time (remember to
plot average 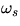 at the middle of the time interval).
Calculate
at the middle of the time interval).
Calculate 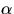 from
the slope. For higher
from
the slope. For higher 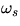 use the stroboscope. To avoid errors from
subharmonics synchronizing with the mark on the shaft, start with the strobe
at too high a frequency. If the synchronization is at the nth
higher
harmonic, you will see the shaft marks appear at n different places.
use the stroboscope. To avoid errors from
subharmonics synchronizing with the mark on the shaft, start with the strobe
at too high a frequency. If the synchronization is at the nth
higher
harmonic, you will see the shaft marks appear at n different places.
- 3.
- Calculate mass of the unweighted torque shaft from observed precessional
angular velocity,
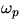 .
Spin the shaft at about
.
Spin the shaft at about  rad/s and minimize nutation by starting
the shaft with a small horizontal (or slightly upward) velocity to
approximate the
rad/s and minimize nutation by starting
the shaft with a small horizontal (or slightly upward) velocity to
approximate the 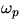 expected. Since the torque
expected. Since the torque
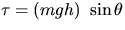 and
and
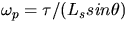 , we predict
, we predict 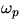 is independent of
is independent of
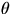 .
Check this experimentally.
With spin angular momentum
.
Check this experimentally.
With spin angular momentum 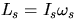 the result is
the result is
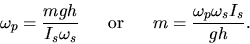
For the shaft mass 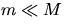 of the ball,
of the ball, 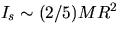 where R is
radius of the ball. Measure the appropriate quantities and calculate m.
Compare with m and h measured directly for an unattached torque shaft.
where R is
radius of the ball. Measure the appropriate quantities and calculate m.
Compare with m and h measured directly for an unattached torque shaft.
- 4.
- Sleeping Top: If
![\begin{displaymath}
\omega_s^2 \;\geq \; 4mgh \left[I_s \; + \; mh^2 \left(\frac{M}{m+M}\right)
\right] / I_s^2 ,\end{displaymath}](img261.gif)
then one can show (see handout) that the gyroscope will spin
without nutation if released carefully
at 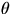 = 0. You can observe the qualitative effect by starting with a
higher
= 0. You can observe the qualitative effect by starting with a
higher 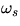 and then gradually slowing down
and then gradually slowing down 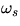 by touching the rotating
ball symmetrically in the horizontal plane until
by touching the rotating
ball symmetrically in the horizontal plane until 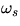 becomes critical
when the shaft will suddenly fall out of the vertical line. Calculate and
check this critical
becomes critical
when the shaft will suddenly fall out of the vertical line. Calculate and
check this critical 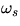 .
.
OPTIONAL:
Nutation frequency, 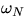 : One can show (see handout) that:
: One can show (see handout) that:
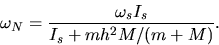
Check this expression when  rad/s. If one has time, change
m and h by adding torque weights and check the new ratio of
rad/s. If one has time, change
m and h by adding torque weights and check the new ratio of
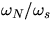 .
.
Amplitude of nutation: The handout shows that the
amplitude of nutation varies as 1/Ls2. Since 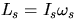 ,
spinning the
gyroscope faster should reduce nutation amplitude at the same time the
nutation frequency increases. Check this at least qualitatively.
Use strobe to measure high
,
spinning the
gyroscope faster should reduce nutation amplitude at the same time the
nutation frequency increases. Check this at least qualitatively.
Use strobe to measure high 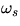 .
.




Next: MC-14-Elastic and Inelastic Collisions
Up: PHYS 201/202 and 207/208
Previous: M-12 Torsion Pendulum and Shear
Michael Winokur
4/7/2000
![$\textstyle\parbox{5.3in}{
\item[ii.] Place one of the supplied weights into the...
...you should make.
The experiments in the Mitac Manual are good possibilities. }$](img246.gif)
![\includegraphics [height=3.3in]{figs/m13-01.eps}](img248.gif)

![\includegraphics [height=0.6in]{figs/m13-02.eps}](img250.gif)
![\includegraphics [height=0.6in]{figs/m13-03.eps}](img251.gif)
![\includegraphics [height=0.6in]{figs/m13-04.eps}](img252.gif)
![]()
![]()
![]()
![]() ,
spinning the
gyroscope faster should reduce nutation amplitude at the same time the
nutation frequency increases. Check this at least qualitatively.
Use strobe to measure high
,
spinning the
gyroscope faster should reduce nutation amplitude at the same time the
nutation frequency increases. Check this at least qualitatively.
Use strobe to measure high ![]() .
.