



Next: M-11 Young's Modulus of
Up: PHYS 201/202 and 207/208
Previous: MC-9 Angular Acceleration and Rotational
APPARATUS: Prony brake, scale, timer, stopwatch, 15 meter tape.
Part A - POWER
- 1.
- Measure your horsepower (1 hp = 746 watts)
by use of the Prony brake which is mounted on
the wall. Try a slow rate that you could keep up all day and another as fast
as you can turn the wheel. Figure out what data are required and how to use
them. Check with your instructor to be sure you have analyzed the problem
correctly. Many calculate the frictional force incorrectly.
- 2.
- Measure the horsepower you develop running up a flight of
stairs.
Part B - FRICTION
INTRODUCTION:
We measure the
coefficient of kinetic friction, 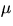 , between rope and wheel of the Prony
brake and test whether
, between rope and wheel of the Prony
brake and test whether 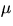 is independent of velocity and of normal force.
(By the way, the Prony brake is named after Gaspard Clair Francois Marie Riche de Prony, who invented it in Paris in
1821 to measure the power of engines. He was the director of the Ecole des Ponts et Chausses, a position he chose over
joining Napoleon's army that invaded Egypt.)
is independent of velocity and of normal force.
(By the way, the Prony brake is named after Gaspard Clair Francois Marie Riche de Prony, who invented it in Paris in
1821 to measure the power of engines. He was the director of the Ecole des Ponts et Chausses, a position he chose over
joining Napoleon's army that invaded Egypt.)
Let f = frictional force/unit length and n = normal
force/unit length
along the rope. For an element 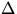 s =
s = 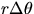 along the rope,
let T'
and T be the tensions at opposite ends of
along the rope,
let T'
and T be the tensions at opposite ends of 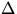 s. For small
s. For small 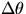 , tensions
, tensions
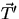 and
and 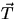 will be almost antiparallel and differ in magnitude,
will be almost antiparallel and differ in magnitude, 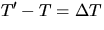 , only by
the frictional force
, only by
the frictional force 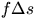 . Thus
. Thus
![\includegraphics [height=2.8in]{figs/m10-1.eps}](img202.gif)
|  |
(1) |
The reaction of the wheel must supply a normal force 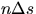 sufficient to
balance the vector sum
sufficient to
balance the vector sum 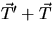 , or
, or
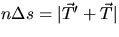 . But from the figure we see that
. But from the figure we see that
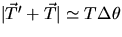 so
so
| 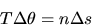 |
(2) |
Eliminating 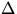 s between (1) and (2) gives
s between (1) and (2) gives 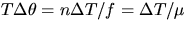 since
since 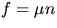 . Hence
. Hence
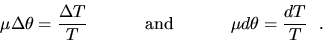
For the Prony brake, we integrate between and 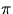 :
:
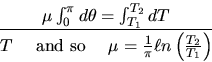
Note #1: While for the Prony brake,
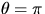 , the general case,
, the general case,
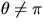 , corresponds to the ``wrapped string tension''
used e.g. for ``warping a ship''. Then
, corresponds to the ``wrapped string tension''
used e.g. for ``warping a ship''. Then 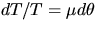 integrates to
integrates to
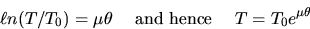
which holds also for a slipping string if 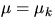 .
.
![\includegraphics [height=2.8in]{figs/m10-2.eps}](img219.gif)
SUGGESTIONS FOR PART B:
- 1.
- Calculate your value of
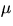 .
. - 2.
- Test whether
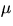 is independent of velocity by turning
at different
speeds and noting that neither T2 nor T1 changes appreciably.
is independent of velocity by turning
at different
speeds and noting that neither T2 nor T1 changes appreciably.
- 3.
- Test whether
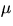 is independent of the normal force by using a
different tension setting for the brake. (Use different link setting in the
chain to vary the tension).
is independent of the normal force by using a
different tension setting for the brake. (Use different link setting in the
chain to vary the tension).
QUESTIONS:
- 1.
- For a stationary wheel the two spring balances will not read the same
if
- (a)
- there are zero errors in the balances,
- (b)
- there is friction in the wheel bearing.
- (c)
- the handle for turning the brake is not directly above or below the
wheel's axis.
Discuss the errors resulting from these effects.
- 2.
- How might one understand a change in
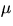 as the normal
force increases
in #3 of Part B?
as the normal
force increases
in #3 of Part B?
Note #2:
Friction arises from intermolecular forces between the atoms (or
molecules) of the two surfaces, and so frictional forces are very
complex. It is therefore surprising that the simple empirical relations
for friction (e.g. that 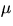 is a constant) hold as well as they do.
is a constant) hold as well as they do.




Next: M-11 Young's Modulus of
Up: PHYS 201/202 and 207/208
Previous: MC-9 Angular Acceleration and Rotational
Michael Winokur
4/7/2000
![]() , between rope and wheel of the Prony
brake and test whether
, between rope and wheel of the Prony
brake and test whether ![]() is independent of velocity and of normal force.
(By the way, the Prony brake is named after Gaspard Clair Francois Marie Riche de Prony, who invented it in Paris in
1821 to measure the power of engines. He was the director of the Ecole des Ponts et Chausses, a position he chose over
joining Napoleon's army that invaded Egypt.)
is independent of velocity and of normal force.
(By the way, the Prony brake is named after Gaspard Clair Francois Marie Riche de Prony, who invented it in Paris in
1821 to measure the power of engines. He was the director of the Ecole des Ponts et Chausses, a position he chose over
joining Napoleon's army that invaded Egypt.)
![]() s =
s = ![]() along the rope,
let T'
and T be the tensions at opposite ends of
along the rope,
let T'
and T be the tensions at opposite ends of ![]() s. For small
s. For small ![]() , tensions
, tensions
![]() and
and ![]() will be almost antiparallel and differ in magnitude,
will be almost antiparallel and differ in magnitude, ![]() , only by
the frictional force
, only by
the frictional force ![]() . Thus
. Thus ![\includegraphics [height=2.8in]{figs/m10-1.eps}](img202.gif)
![]()
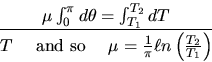
![]() , the general case,
, the general case,
![]() , corresponds to the ``wrapped string tension''
used e.g. for ``warping a ship''. Then
, corresponds to the ``wrapped string tension''
used e.g. for ``warping a ship''. Then ![]() integrates to
integrates to
![]()
![\includegraphics [height=2.8in]{figs/m10-2.eps}](img219.gif)
![]() is a constant) hold as well as they do.
is a constant) hold as well as they do.