



Next: M-10 Power and Friction
Up: PHYS 201/202 and 207/208
Previous: MC-8 The Physical Pendulum
OBJECTIVE:
To study rotational motion resulting from constant torque. Since there
are only six flywheels, groups of up to four will be necessary.
FUNDAMENTAL CONCEPTS:
- 1.
- The equation that
describes the rotational motion of an object
moving with constant angular velocity are completely analogous
to those of linear motion with:
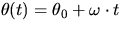 .
.
If you make a plot of 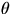 versus t, you find that it describes a
straight line.
The greek letter
versus t, you find that it describes a
straight line.
The greek letter 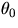 indicates the angular
position of the object at time t=0.
The letter
indicates the angular
position of the object at time t=0.
The letter 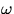 is the slope of the line, and is equal to the
angular velocity of the
object.
is the slope of the line, and is equal to the
angular velocity of the
object.
- 2.
- The equations that describe the rotational motion of an object that
moves with constant angular acceleration are:
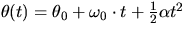 and
and 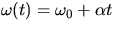 .
.
The greek letter 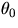 again indicates the angular position of the
object at time t=0.
The letter
again indicates the angular position of the
object at time t=0.
The letter 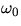 is the
the velocity of the
object at time t=0, and
is the
the velocity of the
object at time t=0, and 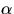 (angular acceleration) is the slope of the graph of
(angular acceleration) is the slope of the graph of 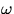 vs t.
vs t.
- 3.
- It is important to stress that the natural units of angular displacement
are in radians and NOT degrees where one full revolution of an object
corresponds to
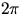 radians or, equivalently, 360o.
Typically units for angular velocity are in rad/sec and for angular
acceleration are in rad/sec2. Notice that the unit dimensions for equivalent
dynamical variables in rotational and linear motion do not match. A linear
velocity can never be compared with a rotational velocity. If you are unclear
with this distinction ask your lab instruction for further clarification.
radians or, equivalently, 360o.
Typically units for angular velocity are in rad/sec and for angular
acceleration are in rad/sec2. Notice that the unit dimensions for equivalent
dynamical variables in rotational and linear motion do not match. A linear
velocity can never be compared with a rotational velocity. If you are unclear
with this distinction ask your lab instruction for further clarification.
APPARATUS:
Basic equipment: Heavy cylindrical flywheel mounted on a low friction bearing
and having a thin hub about which one winds string to hold a weight hanger;
weight hanger and slotted masses.
Computer equipment: Personal computer set
to the M9 lab manual web-page; PASCO interface module; photogate sensor and
extension jack.
Note: If a flywheel needs more than six grams on the end
of string to maintain constant rotational velocity, notify the instructor.
EXPERIMENT I suggested procedures:
- 1.
- Make sure the PASCO interface has been turned on. If not you
will have to reboot the computer. Next make sure that the phone jack connector
from the photogate has been plugged into the extension wire and that the
extension wire phone jack is plugged into the first position in the PASCO
interface module. The computer itself is configured to measure the on/off
timing between two adjacent holes on the wheel (i.e., this gives four timing measurements)
and assumes that there are six holes per revolution. All other dynamical
measurements are based on these input parameters.
- 2.
- Make sure the infrared photogate is properly aligned with the
fly wheel so that the little red LED sensor turns off when all six
drilled holes (in the flywheel) move past the photogate.
- 3.
- To initiate the PASCO interface software you will need to click the
computer mouse when centered on the telescope icon in the ``toolkit'' area
below. The bitmap image below gives a good idea of how the display should
appear. Note that, while you are able to reconfigure the display parameters,
the default values that are specified on start-up should allow you to do this
experiment without necessitating any changes. Three instantaneous
measurements, angular position (
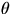 ), velocity (
), velocity (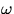 ), and acceleration
(
), and acceleration
(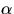 ), are displayed simultaneously in combination with plots of the angular velocity and acceleration. Since
), are displayed simultaneously in combination with plots of the angular velocity and acceleration. Since 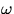 is determined from the position data and
is determined from the position data and
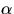 from
from 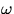 the ``scatter'' in the data will become progressively
more pronounced.
the ``scatter'' in the data will become progressively
more pronounced.
- 4.
- With NO string or weights attached to the flywheel spin the flywheel by
hand so that you obtain approximately one revolution per second. Start the
PASCO data acquisition by CLICKing on the REC icon. To stop it CLICK on the
STOP icon. (Each data run gets its own data set in the ``Data'' display
window. If there are any preexisting data sets you cannot reconfigure either
the interface parameters or sensor inputs.)
- 5.
- Record data for about 60 revolutions of the flywheel and answer the
following questions by using the cross-hair, magnify and rescaling features of the
PASCO plot display. For the statistical analysis you can specify a ``region
of interest'' by clicking to points inside the plot window.
Your lab instructor can provide assistance if necessary.
- (a)
- What was total angular displacement (
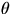 ) of the
wheel?
) of the
wheel?
- (b)
- What were the initial and final angular velocities? Do you observe
any systematic variations?
- (c)
- From these two measurements what was the average angular acceleration?
- (d)
- Does this agree with the average from acceleration plot? USE the
interactive statistical
analysis feature of the plot software to find the mean acceleration.
- (e)
- What was the initial kinetic energy of rotation?
(K.E.
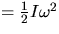 , I=
, I=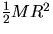 )
) - (f)
- What was the final energy of rotation and energy loss per revolution?
![\begin{figure}
\begin{minipage}
{0.25\linewidth} \hspace*{.4in}
\includegraphics [height=4.5in]{figs/m09_sc.eps}
\end{minipage} \end{figure}](img183.gif)
- 6.
- Repeat the above experiment for 60 revolutions and qualitatively check
(have one lab member count the number of revolutions by brute force)
the computer calibration. Does everything seem consistent?
- 7.
- Predict how many revolutions and how long it will it take for the flywheel
to slow to 75% of its initial angular velocity of 1 rev/sec. What is the
change in kinetic energy?
- 8.
- Now test your prediction by performing this experiment.
EXPERIMENT II Suggested Procedures:
- 1.
- Measuring the angular acceleration
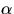
- (a)
- Close the PASCO window and launch the next PASCO application
by CLICKing the
computer mouse when centered on the telescope icon immediately
below.
- (b)
- Take a 2 meter length of string and tie a multiple knot in one end
so that it slides into the slot of the flywheel
inner ring and cannot be easily pulled through. If necessary use a
piece of tape, from the inside, to hold it more securely. On the
other string end tie a loop so that either the 50 gm mass hanger or a
small weight may be hung.
- (c)
- Find the friction correction by hanging small masses on directly on the string (no hanger)
until the tension ``f'' in the string just maintains flywheel rotation
at a constant
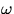 with the string hanging about halfway to the
floor. Obtain the torque applied to the flywheel and compare the
work done in one revolution (
with the string hanging about halfway to the
floor. Obtain the torque applied to the flywheel and compare the
work done in one revolution (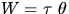 ) to the energy lost
in the Exp. I through the same rotation.
) to the energy lost
in the Exp. I through the same rotation.
Are these two values
comparable?
- (d)
- Replace the small masses with the 50 gm hanger and, with
the string fully extended and hanging vertically, roll the
string up by exactly four full turns of the flywheel. The hanger
should not hit the ground at any time.
- (e)
- Add masses to reach exactly 400 gm and start the data acquisition
while releasing the 400 gm mass. Wait until the mass has both fallen
and risen one time before stopping the scan. Print out one copy of each
curve (three all told) by clicking on the ``File'' menu option and
then clicking on the ``Print All Displays'' button. Use scissors to cut
out each plot and enter it into you lab book labeling all regions of the
position, velocity and acceleration plots.
- (f)
- Determine the angular accelerations,
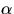 , of the wheel
(falling and rising) and the energy lost (from
, of the wheel
(falling and rising) and the energy lost (from 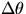 )in this one cycle.
)in this one cycle.
Does this compare favorably with the work done
by the frictional torque?
- (g)
- Repeat the experiment a few more times to ascertain the
reproducibility of
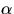 .
. - (h)
- Repeat the last step using a net mass of 200 gm.
- 2.
- Predict
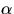 after correcting for friction.
One way to make the calculation follows:
after correcting for friction.
One way to make the calculation follows:
Let I = moment of inertia (calculated from 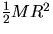
m = mass hung on string (e.g. 200 or 400 grams)
T = tension in the string
f = tension for constant velocity = friction force
r, R = radii of the hub and disc, respectively.
Then the torque on the wheel is 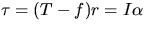 .
.
But F = ma, so 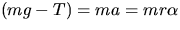 .
.
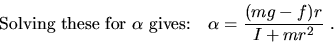
- 3.
- Compare the measured
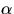 's with the computed values.
Are they consistent within your estimated uncertainties?
's with the computed values.
Are they consistent within your estimated uncertainties?
- 4.
- By drastically increasing the mass added to the hanger deduce
the maximum angular acceleration that the flywheel could receive.
EXPERIMENT III (optional):
Second Measurement of the Flywheel Rotational Inertia
![\begin{figure}
\hspace*{4.5in}
\includegraphics [height=1.9in]{figs/m9-02.eps}
\vspace*{-2.2in} \end{figure}](img189.gif)
- 1.
- Unbalance the flywheel by taping two stacked 100 g masses, m,
on one side near the outside edge of the wheel and at the
same distance from the center, (see figure). The system then
becomes a physical
pendulum and will execute angular simple harmonic motion when displaced
from equilibrium. Be careful that during the oscillatory motion only
one hole moves across the infrared photogate.
If the amplitude of swing is < 10o, the
period, T, of the motion is to sufficient accuracy:
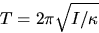
where I = I0 + Im is the total rotational inertia of
the system about the axis of motion, and 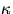 , the torsion constant, is
, the torsion constant, is
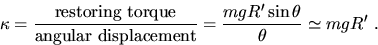
By the parallel axis theorem, Im = Ic + mR'2 where Ic is the
rotational inertia of the added mass m about its own c. of mass. Hence
the rotational inertia of the flywheel, I0, is:
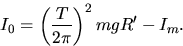
- 2.
- Close the PASCO window and launch the third PASCO application
window by CLICKing on the telescope icon immediately
below.
- 3.
- Measure the period of the pendulum and deduce the rotational
inertia of
the flywheel, I0. Compare with the earlier calculated value.




Next: M-10 Power and Friction
Up: PHYS 201/202 and 207/208
Previous: MC-8 The Physical Pendulum
Michael Winokur
4/7/2000
![\begin{figure}
\begin{minipage}
{0.25\linewidth} \hspace*{.4in}
\includegraphics [height=4.5in]{figs/m09_sc.eps}
\end{minipage} \end{figure}](img183.gif)
![\begin{figure}
\begin{minipage}
{0.25\linewidth} \hspace*{.4in}
\includegraphics [height=2.1in]{figs/m9-01.eps}
\end{minipage} \end{figure}](img185.gif)
![]()
![]() .
.
![]() .
.
![]()
![\begin{figure}
\hspace*{4.5in}
\includegraphics [height=1.9in]{figs/m9-02.eps}
\vspace*{-2.2in} \end{figure}](img189.gif)
![]()
![]()
![]()