



Next: MC-9 Angular Acceleration and Rotational
Up: PHYS 201/202 and 207/208
Previous: MC-7 Simple Pendulum
Do either PART A or PART B but not both!
PART A
OBJECTIVE:
To measure the rotational inertia of a
ring by swinging it as a pendulum from a point of the rim and to compare
the value to that computed.
APPARATUS:
Basic equipment:
Metal rings, (full, half, and quarter rings); knife
edge and 2-point supports.
Computer equipment: Personal computer set
to the M7 lab manual web-page; PASCO interface module; photogate sensor and
extension jack.
INTRODUCTION:
The period of a rigid body swinging on
an axis as a pendulum is (for small amplitudes 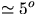 ):
):
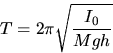
where
REQUIRED INVESTIGATIONS:
- 1.
- Initiate the PASCO interface software by clicking on the telescope
icon below. There will be a just a single table for recording the measured
period.
- 2.
- Measure the period of the ring supported on the knife edge and
swinging in its own plane. From the period calculate I0. Use
the parallel axis
theorem to also calculate Ic,
the rotational inertia about an axis through
the c. of m. and perpendicular to plane of the ring. Compare this
Ic with the computed value of Ic = M (r12 + r22)/2
where the r's are the inner and outer radii of the ring. Do the two
Ic's agree within reasonable experimental error? Explain.
- 3.
- Measure the period of the ring when supported on the two sharp points but
swinging perpendicular to its plane. From this period calculate the rotational
inertia about an axis through those two points. Then use the parallel axis
theorem to find the rotational inertia about a diameter of the ring. How does
this rotational inertia compare with that about an axis perpendicular to the
plane of the ring and through the center of mass?
OPTIONAL PROBLEM:
Prove that this relationship should exist by
calculating the rotational inertias about the two orthogonal axes.
- 4.
- One circular hoop has been cut in sections. Measure the period of
a half-hoop when set at its midpoint on a knife edge; also the
period of a quarter-hoop. (Be sure hoop sections have the same radius of
curvature r).
Proof that any section of a thin hoop has the same
period if oscillating in
the plane of the hoop:
Note that IA= mr2 for any partial hoop.
The parallel axis theorem then gives:

![\includegraphics [height=2.8in]{figs/m8-01.eps}](img160.gif)
Hence
IC = mr2 - mr2 + 2mrh - mh2 = 2mrh - mh2 .
When one substitutes this IC into
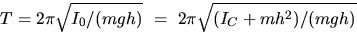
one finds
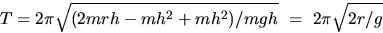
or a period independent of what fraction of a hoop is used!
OPTIONAL PROBLEM:
For a thick hoop, the above relationship
does not hold exactly. Show that the thickness of the laboratory hoops accounts
for the small difference between T for a whole hoop and T for a half hoop.
(This is a rather difficult problem. For the older style laboratory hoops the
finite thickness increases the period by 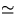 1.8%; the period of the
half-hoop will be
1.8%; the period of the
half-hoop will be 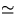 5.2% larger, and the quarter-hoop over 22% longer!)
5.2% larger, and the quarter-hoop over 22% longer!)
PART B of M-8
KATER'S REVERSIBLE PENDULUM
OBJECTIVE:
To study conjugate centers of oscillation and to measure g accurately.
APPARATUS:
Long rod with movable weights and knife edges; bearing
surface (Kater's pendulum mount); infrared photogate & support stand;
computer equipment as in PART A.
INTRODUCTION:
![\includegraphics [height=2.8in]{figs/m8-02.eps}](img165.gif) When swung from O the period is:
When swung from O the period is:
By substitution one easily verifies that T0 = TP for two arrangements:
1) the trivial solution h0 = hP, and
2) when IC = mh0hP.
For the second case:
| 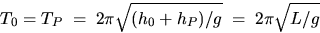 |
(1) |
where O and P are conjugate centers of oscillation.
(See note at end of experiment.) A
measurement of the period (T) and distance
(L = h0 + hP) between knife edges then gives an
accurate value of g.
Empirically finding an L to give T0 = TP is
tedious. Instead, find an L for which 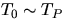 and then eliminate
IC
from the first two equations above to give:
and then eliminate
IC
from the first two equations above to give:
| 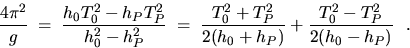 |
(2) |
If one chooses an asymmetric geometry for the location of the weights, one can
avoid 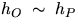 .Note then that for
.Note then that for 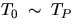 the first term
dominates, and an accurate value of g
results if one knows accurately L = h0 + hP,
(the distance between the
knife edges), and to much less accuracy the difference h0 - hP.
the first term
dominates, and an accurate value of g
results if one knows accurately L = h0 + hP,
(the distance between the
knife edges), and to much less accuracy the difference h0 - hP.
SUGGESTED PROCEDURE:
- 1.
- Find the approximate c. of m. of the pendulum plus asymmetrically located
weights. Then set one knife edge as far from the c. of m. as feasible. This
avoids
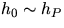 which would make the last term of Eqn. 2 large.
which would make the last term of Eqn. 2 large.
NOTE: Keep
this knife edge position fixed through out the experiment.
- 2.
- Determine the period of the pendulum, T0, when swinging from this
knife edge. Keep amplitude small (< 5o)
and use a photogate timer.
- 3.
- Calculate the length, L, of a simple pendulum
to give the same period.
- 4.
- Set the second knife edge at this distance L from the first knife
edge.
- 5.
- Determine the new period of the pendulum, TP, for swinging from the
second knife edge. This period TP will not quite equal T0 since
moving the second knife edge has changed slightly the c. of m. and hence
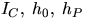 , and also both T0 and TP.
, and also both T0 and TP.
- 6.
- Recalculate the length L of the equivalent simple pendulum to give
this new period TP. Then reset the knife edge accordingly.
- 7.
- Redetermine the period about the first knife edge.
- 8.
- One can continue this iterative process (6 thru 7) until the
two periods are arbitrarily close to each other, and hence g is given by
Eqn. 1. However this is not necessary if one accurately finds the
new c. of m. (e.g. by balancing the
pendulum on the knife edge for the hoops of M-8A)
and then uses Eqn. 2.
- 9.
- Estimate your uncertainty in g and compare with accepted
value (see M-4).
----------------------
Note (from p. 38): these two conjugate centers of oscillation (O
and P)
exist of course for any
rigid physical pendulum, e.g. a baseball bat:
Let one center of oscillation be where the batter grasps the bat.
The conjugate center of oscillation is then called the center of
percussion because if the ball hits the bat at this point, the blow
rotates the bat about the other center of oscillation, (i.e. the batter's
hands) and so the bat transmits no ``sting" to the hands. However, if the ball
hits very far from the center of percussion, the hands
receive much of the blow and an unpleasant ``sting'' can result.




Next: MC-9 Angular Acceleration and Rotational
Up: PHYS 201/202 and 207/208
Previous: MC-7 Simple Pendulum
Michael Winokur
4/7/2000
![]() ):
):
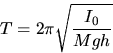
![]()
![\includegraphics [height=2.8in]{figs/m8-01.eps}](img160.gif)
![]()
![]()
![]() 1.8%; the period of the
half-hoop will be
1.8%; the period of the
half-hoop will be ![]() 5.2% larger, and the quarter-hoop over 22% longer!)
5.2% larger, and the quarter-hoop over 22% longer!)
![\includegraphics [height=2.8in]{figs/m8-02.eps}](img165.gif) When swung from O the period is:
When swung from O the period is:
![]() and then eliminate
IC
from the first two equations above to give:
and then eliminate
IC
from the first two equations above to give:
![]() .Note then that for
.Note then that for ![]() the first term
dominates, and an accurate value of g
results if one knows accurately L = h0 + hP,
(the distance between the
knife edges), and to much less accuracy the difference h0 - hP.
the first term
dominates, and an accurate value of g
results if one knows accurately L = h0 + hP,
(the distance between the
knife edges), and to much less accuracy the difference h0 - hP.