Overview: Remember that ``rms'' value of the AC voltage or current means the ``root-mean-square'' and this value is useful even when the voltage or current is changing but not as perfect sine waves. For example, the voltage used to provide power for most lights and appliances is roughly
The rms concept allows us to describe any AC voltage as having a particular rms voltage and a particular phase.
In this experiment we will use the subscript ``rms'' for some measurements and will
use ``![]() '' or ``
'' or ``![]() '' or ``
'' or ``![]() '' or ``
'' or ``![]() '' without this subscript when referring to
instantaneous values of the voltage or current. Thus, even if two rms voltages
are equal, (
'' without this subscript when referring to
instantaneous values of the voltage or current. Thus, even if two rms voltages
are equal, (
![]() ),
), ![]() may not be equal to
may not be equal to ![]() since
since ![]() and
and ![]() may have different phases.
may have different phases.
The impedance ![]() (in ohms) of any part of a circuit is the ratio of the rms voltage across that
part and the rms current though that part:
Because impedance is defined as a ratio of voltage/current, impedance is measured in ohms.
If
(in ohms) of any part of a circuit is the ratio of the rms voltage across that
part and the rms current though that part:
Because impedance is defined as a ratio of voltage/current, impedance is measured in ohms.
If ![]() and we measure
and we measure ![]() and
and ![]() in henries and farads,
respectively, then it can be shown
that the impedance
in henries and farads,
respectively, then it can be shown
that the impedance ![]() of an resistance
of an resistance ![]() is
is ![]() and the impedance
and the impedance ![]() (in ohms) of an inductance
(in ohms) of an inductance ![]() is
is
![]() .
and the impedance
.
and the impedance ![]() (in ohms) of a capacitance
(in ohms) of a capacitance ![]() is
is
![]() .
It can also be shown that the impedance Z (in ohms) of
an RLC series circuit (shown in Fig. 1) is
.
It can also be shown that the impedance Z (in ohms) of
an RLC series circuit (shown in Fig. 1) is
where,
The impedance ![]() of the RLC series circuit is a minimum for
of the RLC series circuit is a minimum for ![]() .
The frequency for which this occurs is the resonant frequency. At this
frequency,
.
The frequency for which this occurs is the resonant frequency. At this
frequency, ![]() , the current thru R is maximum, but the voltage
, the current thru R is maximum, but the voltage ![]() across the LC series combination is a minimum and in fact would be zero
if the inductor had no resistance. Hence one can search for
across the LC series combination is a minimum and in fact would be zero
if the inductor had no resistance. Hence one can search for ![]() by
varying the frequency and looking either
by
varying the frequency and looking either
1) for a maximum ![]() signal, or 2) a minimum
signal, or 2) a minimum ![]() signal.
signal.
A search for the minimum
has a practical advantage that near the resonant frequency, ![]() , one can
increase enormously the detection sensitivity by going to maximum signal
generator amplitude and also by going to higher scope gain.
, one can
increase enormously the detection sensitivity by going to maximum signal
generator amplitude and also by going to higher scope gain.
Our dual trace scope allows the simultaneous observation of two voltages. If we use differential amplifiers (E-8) to avoid ground problems, then we can compare the signal across the resistor (displayed on one trace) with the signal across other circuit elements (displayed on the other trace). Since across a resistor the voltage and current are in phase, and since the current throughout a series circuit is the same, we can observe the relative phase relationship between the current and any other measured voltage.
![\includegraphics[width=4.0in]{figs/e9-01.eps}](img239.png)
![\includegraphics[width=2.4in]{figs/e9-02.eps}](img251.png)

![\begin{displaymath}Z = R\left[ 1 + Q^2\left( \frac{f}{f_{r}} - \frac{f_r}{f}\right) ^2\right]
^{1/2}.\end{displaymath}](img256.png)
![\includegraphics[width=6.0in]{figs/e9-03a.eps}](img261.png)
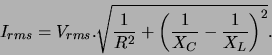
![\includegraphics[width=6.0in]{figs/e9-04.eps}](img280.png)