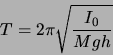
where

Do either PART A or PART B but not both!
OBJECTIVE:
APPARATUS:
INTRODUCTION:
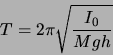

REQUIRED INVESTIGATIONS:
Proof that any section of a thin hoop has the same period if oscillating in the plane of the hoop:
|
|
|
OPTIONAL PROBLEM:
APPARATUS:
INTRODUCTION:
|
|
By substitution one easily verifies that
1) the trivial solution
2) when
For the second case:
Empirically finding an |
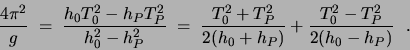 |
(2) |
SUGGESTED PROCEDURE:
Let one center of oscillation be where the batter grasps the bat. The conjugate center of oscillation is then called the center of percussion because if the ball hits the bat at this point, the blow rotates the bat about the other center of oscillation, (i.e. the batter's hands) and so the bat transmits no ``sting" to the hands. However, if the ball hits very far from the center of percussion, the hands receive much of the blow and an unpleasant ``sting'' can result.