



Next: MC-1b Errors and the Density
Up: MC-1 Errors & Motion
Previous: MC-1 Errors & Motion
OBJECTIVES:
The major objectives of this first, short (est. 1 hr) computer lab
are to begin to develop
an understanding of what it means to make an experimental measurement and
provide a methodology for assessing random and systematic errors in this
measurement
process. In addition this lab will also give you a minimal framework
in which to introduce you to the
PASCO© (page ![[*]](/usr/local/lib/latex2html-97.1/icons.gif/cross_ref_motif.gif) ) interface hardware and software.
) interface hardware and software.
THEORY:
By now you should have had numerous opportunities to become familiar with time
and the concept of a time interval. The increment of one second will be used
as an intuitive reference point. In this lab you will test your ability to
internalize this one second time interval by making and recording a repetitive
flicking motion with your finger. By flicking your finger back and forth
you will move it though an infrared beam sensor (i.e. the PASCO photogate)
and each full cycle (back and forth, approximately 2 seconds)
will be simultaneously recorded, plotted and tabulated
by the PASCO interface software.
Your goal in this experiment is to assess the size of systematic and random
errors in your data set and learn a simple methodology for
distinguishing between the two.
SYSTEMATIC ERRORS: These are errors which affect the accuracy of a
measurement. Typically they are reproducible so that they always affect the
data in the same way. For instance if a clock runs too slow you will make
a time measurement which is less than the actual reading.
RANDOM ERRORS: These are errors which affect the precision of a
measurement. A process itself may have a random component (as in radioactive
decay) or the measurement itself may be technique limited which causes the
reading to fluctuate. If many measurements are made then a statistical
analysis of this data may be made and these errors minimized.
NOTE: In precision measurements it can be very difficult to isolate an
eliminate errors, especially systematic errors.
APPARATUS:
- Computer with monitor, keyboard and
mouse.
- A PASCO photogate and stand:
This device emits a narrow infrared beam in the gap and occluding the beam
prevents
it from reaching a photodetector. When the beam is interrupted the red LED
should become lit. (Plugged into DIGITAL CHANNEL #3.)
- A PASCO Signal Interface (CI-700)
monitors the photodetector output vs time and can be configured to
tabulate, plot and analyze this data.
PROCEDURE:
To configure the experiment you should refer to Fig. 1 below. Adjust the photogate so
that one member can easily and repetitively flick his/her finger through the
gap. The phone-jack cable from the photogate should be plugged into the
DIGITAL CHANNEL #3 socket. Ignore the other sensors which may already be
plugged into other sockets. It is important PASCO interface is turned
on before the computer. If not the computer will not recognize it and,
therefore, it must be rebooted to properly communicate with the PASCO module.
Figure 1:
A schematic of the M0C components.
![\begin{figure}
\centering
\includegraphics [height=2.0in]{figs/m00-1.eps}
\end{figure}](img72.gif) |
To initiate the PASCO (page ![[*]](/usr/local/lib/latex2html-97.1/icons.gif/cross_ref_motif.gif) ) interface software you will
need to click the computer mouse when centered on the telescope icon in the
``toolkit'' area below. The bitmap image below gives a good idea of how the
display should appear. Note that, while you are able to reconfigure the display
parameters, the default values that are specified on start-up will allow you to
do most of this experiment without necessitating any major changes.
) interface software you will
need to click the computer mouse when centered on the telescope icon in the
``toolkit'' area below. The bitmap image below gives a good idea of how the
display should appear. Note that, while you are able to reconfigure the display
parameters, the default values that are specified on start-up will allow you to
do most of this experiment without necessitating any major changes.
You will note that a ``dummy'' first data set already exists on start-up
showing a typical data run. In the table you can view all 35 data points
and the statistical analysis, including mean and standard deviation.
In addition there should be a plot of this data and a histogram.
Figure 2:
The PASCO SCIENCE WORKSHOP display window
![\begin{figure}
\centering
\includegraphics [height=4.0in]{figs/mc0-02.eps}
\end{figure}](img73.gif) |
SUGGESTED PROCEDURE:
- 1.
- Start the preliminaries by CLICKing on the MON icon and practice
``flicking'' a finger back and forth so that a two second interval
appears in the window. CLICK on the STOP icon when done. (The upper
left window is configured like a tape player). The same person need
not perform both operations.
- 2.
- Start the data run CLICK on the REC icon and stop it by CLICKing
on the STOP icon. Each run gets
its own data set in the ``Data'' display window.
(If there are any data sets in existence
you will not be able to reconfigure the interface
parameters or sensor inputs.)
- 3.
- With the REC option on, cycle a finger back and forth fifty times and
STOP the data acquisition. DO NOT watch the time display while you do this.
- 4.
- What is the mean time per cycle? What is the standard deviation?
The mean
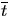 and standard deviation
and standard deviation 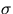 are given by:
are given by:
![\begin{displaymath}
\overline{t}= \sum_{i=1}^N t_i/N \mbox{~~~and~~~~}
\sigma = \sqrt{{\sum_{i=1}^N (t_i-\overline{t})^2}/[N-1]}~~. \end{displaymath}](img75.gif)
Questions to consider:
I. Is your mean suggestive of a systematic error?
II. Does your data qualitatively give the appearance of a normal
distribution (i.e. a Gaussian bell curve.)
- 5.
- For analyzing and quantifying the random errors one interested in
assessing how
a data set is distributed about the mean. The standard deviation
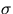 is
one common calculation that does this. In the case of a normal
distribution approximately 70% of the data points fall within
is
one common calculation that does this. In the case of a normal
distribution approximately 70% of the data points fall within 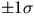 of
the mean (90% within
of
the mean (90% within 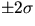 ).
Is your data consistent with this attribute?
).
Is your data consistent with this attribute?
- 6.
- Assessing the possibility of systematic behavior is somewhat more subtle.
In general
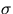 is a measure of how much a single measurement
fluctuates from the mean. In this run you have made fifty presumed identical
measurements. A better estimate of how well you have really determined the
mean is to calculate the standard deviation of the mean
is a measure of how much a single measurement
fluctuates from the mean. In this run you have made fifty presumed identical
measurements. A better estimate of how well you have really determined the
mean is to calculate the standard deviation of the mean
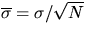 . After recording
. After recording 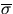 in
you lab book, can you now observe any evidence that there is a systemic error
in your data? Answer this same question with respect to the first ``sample''
data set.
in
you lab book, can you now observe any evidence that there is a systemic error
in your data? Answer this same question with respect to the first ``sample''
data set.
- 7.
- OPTIONAL: Systematic errors can sometimes drift over time. In the best-case
scenario they drift up and down so that they hopefully average out to zero.
(Clearly it would be better if they could be eliminated entirely.)
With respect to
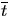 and
and 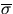 for the first 25 and
second 25 cycles do you observe any systematic trends. Use the ``region of
interest'' feature of the statistical analysis software by using the mouse
and highlighting (in black) data subset (through a CLICK and drag motion) over
the rows of interest.
for the first 25 and
second 25 cycles do you observe any systematic trends. Use the ``region of
interest'' feature of the statistical analysis software by using the mouse
and highlighting (in black) data subset (through a CLICK and drag motion) over
the rows of interest.




Next: MC-1b Errors and the Density
Up: MC-1 Errors & Motion
Previous: MC-1 Errors & Motion
Michael Winokur
4/7/2000
![\begin{figure}
\centering
\includegraphics [height=2.0in]{figs/m00-1.eps}
\end{figure}](img72.gif)
![\begin{figure}
\centering
\includegraphics [height=4.0in]{figs/mc0-02.eps}
\end{figure}](img73.gif)
![\begin{displaymath}
\overline{t}= \sum_{i=1}^N t_i/N \mbox{~~~and~~~~}
\sigma = \sqrt{{\sum_{i=1}^N (t_i-\overline{t})^2}/[N-1]}~~. \end{displaymath}](img75.gif)