S-2  Velocity of Sound in Air

OBJECT:

  To calculate the velocity of sound from measurement of the wavelength in air for sound of a certain frequency.

APPARATUS:

  Resonance tube with arrangement for varying water level (use only distilled water); rubber tipped hammer; tuning fork; Hg thermometer.

INTRODUCTION:

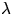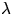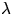  For a closed tube, resonance occurs at tube lengths of an odd multiple of one-fourth wavelength, i.e. at $\lambda$/4, 3$\lambda$/4, 5$\lambda$/4 etc.

SUGGESTIONS:

 

1.

Find the positions of the water level in the tube for the first three of these resonances. Use these readings to calculate the velocity of sound, v. Initially have enough water that you can raise the level above the first resonance position. The tuning fork frequency is on the fork.

Since the effective end of the resonance tube is not at the tube's end, do not use the position of the tube's top in your calculations, but rather take differences between the other readings.

2.

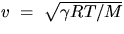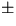Since v = , correct your value of v to 0^oC (T = 273.16 K) and compare with that accepted for dry air at 0^oC: 331.29 $\pm$ .07 m/s, [Wong, J. Acoust. Soc. Am., 79, 1559, (1986)]. For humid air see 3. below.

3.

How should the v.p. of water, P_w, in the tube affect the measured velocity? An estimate is not difficult from v = 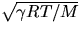$\sqrt{\gamma RT/M}$.Use an average 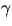$\gamma$/M:

$<\gamma/M\gt~=~\left[ (\gamma _{a}/M_{a})P_{a}~+~ (\gamma _{w}/M_{w})P_{w}\right] (P_{a} + P_{w})$

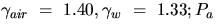where $\gamma _{air}~=~1.40, \gamma _{w}~=~1.33; P_{a}$is the partial pressure of air and P_w is the v.p. of water; M_a 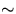$\sim$ 29 kg and M_w = 18 kg. Hence

$v_{dry}~\cong ~v_{humid}\sqrt (\gamma _{a}/M_{a})/< \gamma /M\gt$

OPTIONAL: Humidity changes will affect tuning of what musical instruments?

4.

What effect does atmospheric pressure have on the velocity of sound in dry air? (Assume air at these pressures is an ideal gas.)

5.

Viscosity and heat conduction in the tube may reduce v by 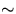$\sim$0.1%. See N. Feather, ``The Physics of Vibrations and Waves'', Edinburgh Univ. Press, (1961), p. 110-120; this reference also has a delightful historical account (including Newton's famous goof).