



Next: SC-1 Transverse Standing Waves on
Up: H-2 Latent Heat
Previous: H-2a Latent heat of fusion
OBJECTIVE:
To measure the heat of vaporization of liquid nitrogen, Lv,
at its boiling point (Tb = 77 K at standard atmospheric pressure).
APPARATUS:
Dewar flask; liquid nitrogen (ask for help in
getting it from a large storage Dewar opposite room
4411 Sterling); aluminum cylinder on
a long thread; double pan balance; calorimeter plus
water jacket for thermal ballast (as in H-2a); timer;
thermocouple type digital thermometer; selection of slotted masses; coffee
pot for hot water.
PRECAUTIONS:
Liquid N2 is fascinating to work with. However, keep in mind the following simple safety precautions.
- 1.
- Never stopper a flask of liquid N2 with an unperforated stopper.
- 2.
- Have a perforated stopper on the Dewar throughout the experiment to
prevent condensation of moisture from the air on the inside of the flask.
- 3.
- Avoid prolonged contact of liquid N2 with your skin.
The insulating vapor layer may disappear and severe frost-bite may result.
INTRODUCTION:
When one lowers
an aluminum cylinder of mass, mAl, and at room
temperature, Tr, into liquid N2 at its boiling
temperature, Tb, the cylinder cools to Tb. The heat given off during
this cooling, QAl, will vaporize a mass mN of liquid N2.
You might expect to find Lv, of the
nitrogen by setting
mNLv = QAl = mAlcAl(Tr - Tb) .
This method fails because cAl is not constant over the
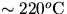 temperature range between Tr and Tb.
See figure 1.
temperature range between Tr and Tb.
See figure 1.
We can avoid this difficulty by noting that
QAl is also the heat needed
to warm the same aluminum cylinder
to from Tb to Tr. You can measure this heat by placing
the cold aluminum cylinder (at temperature Tb) in a
``calorimeter'' that contains water and
observing the change in temperature of the water, 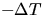 ,
-provided that the
final temperature of the water, Tf, is room temperature,
Tr. It is hard to arrange for Tf to end up exactly at room temperature, but if Tf is close to Tr, one can accurately correct the calorimeter data for the small
additional heat term, namely mAlcAl(Tr - Tf),
since over the small
Tr -Tf interval,
,
-provided that the
final temperature of the water, Tf, is room temperature,
Tr. It is hard to arrange for Tf to end up exactly at room temperature, but if Tf is close to Tr, one can accurately correct the calorimeter data for the small
additional heat term, namely mAlcAl(Tr - Tf),
since over the small
Tr -Tf interval, 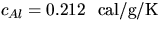 is constant.
is constant.
Figure 1:
Specific heat capacity of Al vs. temperature.
![\begin{figure}
\centering
\includegraphics [width=5.2in]{figs/fhc2b-3.eps}
\\ \end{figure}](img367.gif) |
SUGGESTIONS ON PROCEDURE:
- 1.
- To maximize sensitivity (i.e. to get a large temperature change in the water) use only enough water (
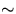 125-150 grams)
in the calorimeter to cover the metal cylinder.
125-150 grams)
in the calorimeter to cover the metal cylinder.
- 2.
- The calorimeter is designed to thermally isolate the water from the surroundings. The inner vessel of the calorimeter is mounted within, but thermally isolated from, a surrounding water jacket, which is close to room temperature. The isolation isn't perfect, so here will be some small amount of heat flow between the calorimeter and the jacket. To minimize the net heat exchange with the water jacket, you will want to make the initial water temperature as far above the jacket temperature as you expect it to end up
below the jacket temperature after the water in the inner vessel has been cooled by your Al cylinder. (The jacket temperature will remain fairly constant during the experiment.) Estimate roughly the proper initial water and calorimeter temperature.
[Use the measured mass of the aluminum cylinder, mAl, its specific heat (0.212
kcal/kgoC) and the b.p. of liquid N2,
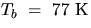 . For this rough calculation, assume that the specific heat of Al
. For this rough calculation, assume that the specific heat of Al 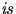 constant with temperature.]
Determine the water mass, mw, and appropriate starting temperature.
constant with temperature.]
Determine the water mass, mw, and appropriate starting temperature.
- 3.
- Place the flask containing liquid nitrogen (plus perforated stopper) on
one pan of a balance and record the mass each minute for 10 minutes. (Why is
the mass decreasing?)
- 4.
- Record the temperature of the metal cylinder,
TR, and then lower it (by a thread) gently to the bottom of the flask.
Replace the stopper (perforated) on the top of the flask and continue recording
the total mass each minute until it shows a slow steady decrease.
- 5.
- Record the initial temperature, Ti, of
the calorimeter, which you have chosen so cleverly in section 2. Transfer the
cold metal cylinder
into the calorimeter, and note the
calorimeter temperature every two minutes (while gently stirring). Record
the mass of the flask of liquid N2
on alternate minutes. When the calorimeter temperature has reached
a slow steady rate of change and the mass of the flask of liquid N2 is
falling at a slow steady rate, discontinue the readings.
- 6.
- Plot the mass of the flask plus nitrogen as a function of time. For
the minutes that the cylinder of metal was in the flask, subtract the mass of the
cylinder. See figure for a typical plot.
![\includegraphics [width=2.6in]{figs/l103/h04-2.eps}](img370.gif) How much of the N2 mass change
was caused by the heat from the cylinder? If a-b and c-d were parallel, it
would be the vertical distance between these lines. But
c-d ordinarily has a smaller slope than a-b, possibly because
the evaporation of liquid nitrogen between b and c has cooled the
upper part of the flask.
How much of the N2 mass change
was caused by the heat from the cylinder? If a-b and c-d were parallel, it
would be the vertical distance between these lines. But
c-d ordinarily has a smaller slope than a-b, possibly because
the evaporation of liquid nitrogen between b and c has cooled the
upper part of the flask.
Hence we use the average of the two rates of fall by drawing
a vertical line through e, (the midpoint of line b-c). Then f-g
estimates the mass, mN, evaporated by the heat from the cylinder.
- 7.
- The final temperature, Tf, of the Al cylinder in the calorimeter usually
will not be quite the same as the initial temperature (= Tr) of the cylinder
before it was lowered into the liquid nitrogen.
Hence QAl will be the heat to warm the Al cylinder
in the calorimeter to Tf plus the mass of the
cylinder 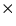 (specific heat of aluminum)
(specific heat of aluminum) 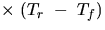 .
.
Specifically if:
Lv = latent heat of vaporization of nitrogen
mN = mass of nitrogen evaporated by heat from the cylinder
mAl, cAl = mass and specific heat of Al cylinder
Ti = initial temperature of water and calorimeter
mw, cw = mass and specific heat of water
mc, cc = mass and specific heat of calorimeter and stirrer
ht = heat capacity of immersed part of thermometer,
then, if we neglect ht:
QAl = mN Lv = (mw cw + mc cc) (Ti - Tf)
+ mAl cAl (Tr - Tf) .
Calculate Lv from the above relation.
The accepted value is 47.8 kcal/kg.
OPTIONAL:
- 1.
- Calculate the apparent specific heat of the Al block by use of
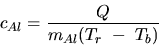
and your data. How does your result compare with the accepted
value of cAl = 0.212 kcal/kg? Explain. (See Introduction).
- 2.
- Observe (but do not touch) the following items after immersion in
liquid N2: rubber (get a piece from the instructor), pencil eraser.
- 3.
- Pour a little liquid N2 onto the floor. Explain the behavior of
the small spheres of liquid N2.
H5 Mechanical Equivalent of Heat
Equipment for this experiment is not currently available. For a write up
of H5 consult lab manuals  1988.
1988.




Next: SC-1 Transverse Standing Waves on
Up: H-2 Latent Heat
Previous: H-2a Latent heat of fusion
Michael Winokur
4/7/2000
![]() ,
-provided that the
final temperature of the water, Tf, is room temperature,
Tr. It is hard to arrange for Tf to end up exactly at room temperature, but if Tf is close to Tr, one can accurately correct the calorimeter data for the small
additional heat term, namely mAlcAl(Tr - Tf),
since over the small
Tr -Tf interval,
,
-provided that the
final temperature of the water, Tf, is room temperature,
Tr. It is hard to arrange for Tf to end up exactly at room temperature, but if Tf is close to Tr, one can accurately correct the calorimeter data for the small
additional heat term, namely mAlcAl(Tr - Tf),
since over the small
Tr -Tf interval, ![]() is constant.
is constant. ![\includegraphics [width=2.6in]{figs/l103/h04-2.eps}](img370.gif) How much of the N2 mass change
was caused by the heat from the cylinder? If a-b and c-d were parallel, it
would be the vertical distance between these lines. But
c-d ordinarily has a smaller slope than a-b, possibly because
the evaporation of liquid nitrogen between b and c has cooled the
upper part of the flask.
How much of the N2 mass change
was caused by the heat from the cylinder? If a-b and c-d were parallel, it
would be the vertical distance between these lines. But
c-d ordinarily has a smaller slope than a-b, possibly because
the evaporation of liquid nitrogen between b and c has cooled the
upper part of the flask. ![]() (specific heat of aluminum)
(specific heat of aluminum) ![]() .
.
![]()
![]() 1988.
1988.