



Next: H-2 Latent Heat
Up: PHYS 201/202 and 207/208
Previous: MC-15b Simple Harmonic Motion and
OBJECTIVES:
To observe the behavior of
an ``ideal'' gas (air) and to determine absolute zero (in Celsius).
FUNDAMENTAL CONCEPTS:
The behavior of an ideal gas under varying
conditions of pressure and
temperature is described
by the ``Ideal Gas Law'':

Where
P is the pressure (in Pascals, Pa),
V is the volume (in m3), T is the temperature in Kelvins (K= C+ 273),
n is the number of moles present (1 mole 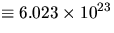 ),
and R is the gas constant (
),
and R is the gas constant (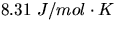 ).
).
This equation is a combination of two laws which were discovered previously:
- 1.
- Boyle's Law relates volume and pressure of a fixed quantity of
gas at a constant temperature: PV = constant
- 2.
- Charles' Law relates volume and temperature of a fixed quantity of
gas at a constant pressure V/T = constant
Gay-Lussac finally combined the two laws into the ideal gas law shown in
Eqn. 1.
In EXPT. I Boyle's law will be verified by varying V and P (assuming fixed T).
In EXPT. II You will vary T and V to determine the value of absolute zero.
APPARATUS:
Basic equipment: EXPT. I - Lab stand; 60 cm3 plastic syringe attached
to a plastic ``quick-connect'' coupling.
EXPT. II - PASCO Steam generator; water jacket container;
steel Dewar flask; small stainless steel can with a volume
of 98 cm3 with a ``quick release''
connector; FLUKE digital thermometer and temperature probe
Computer equipment: Personal computer set
to the HC1 lab manual web-page; PASCO interface module; PASCO pressure sensor
(mounted on lab stand).
EXPERIMENT I: BOYLE'S LAW
- 1.
- CLICK on the telescope icon below to initiate the PASCO
 interface software. The computer, monitor and PASCO interface
must already be on and pressure sensor plugged into the A DIN connector
position. (If not see your instructor.)
interface software. The computer, monitor and PASCO interface
must already be on and pressure sensor plugged into the A DIN connector
position. (If not see your instructor.)
- 2.
- The PASCO software window should display graphs configured to
display pressure vs volume and pressure vs inverse volume, a
table for these three values, a panel meter for the instantaneous pressure
reading.
Since there is no automated volume
measurement will have to enter these data points manually.
NOTE: The volume is recorded in
milliliters (1 mL = 1 cm3) and the pressure in kilopascals
(kPa). In this case the ideal gas law (PV=nRT, T in Kelvin) uses
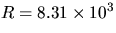 (kPa
(kPa cm3)/(mol
cm3)/(mol K).
K).
- 3.
- If the syringe is attached the the pressure disconnect it at the
twist-lock quick connect coupling.
Set the syringe plunger to the 60 cm3 mark and then
reconnect it to the pressure sensor.
Make sure that the equipment looks as sketched below.
Figure 1:
Sketch of pressure sensor and syringe/plunger assembly.
![\begin{figure}
\centering
\includegraphics [width=3.2in]{figs/hc1-01.eps}
\\ \vspace*{-.1in}\end{figure}](img356.gif) |
- 4.
- Initiate the data acquisition by clicking on the REC button in the
upper left panel a large window for keyboard entry will appear (i.e. Keyboard Sampling).
There is no automated volume
measurement for the plunger position so you will use the keyboard to enter data points manually.
Slowly push the plunger in to the 50 cm3 position (about
10 seconds) and back to the original setting while watching the panel pressure
meter and record in your lab-book the readout precision of the pressure sensor.
- 5.
- Now begin the actual data logging by clicking the mouse on the
numeric entry field in the Keyboard Sampling window, replacing the
current value with 60.0 and then striking the Enter key. Data logging
should be confirmed by observing a new data point on the plots and three
new values in first row of the table. The PASCO software will try to
anticipate your next volume setting in the Keyboard Sampling window.
You should change this value to the appropriate value before logging your
next data point.
- 6.
- Reduce the volume slowly in discrete 5 cm3 increments while logging
the data at each step (see the previous item) until you reach 20 cm3. Then
slowly increase the volume in 5 or 10 cm3 steps (remember to log the
data) until you reach 60 cm3.
- 7.
- Stop the data acquisition and transfer your
data to a table in your write-up and comment on the
reproducibility of your measurements. Do your plots have the correct
functional behavior? Your can refrain from printing out the graphs until
your have performed a linear regression using either the PASCO graphical
analysis capabilities or the Vernier GA graphical analysis package.
- 8.
- Which of the two graphs do you expect to be a line and why? For this ``curve'' what is the
expected y intercept? Now fit this data to a line (using linear regression) and record the slope
and intercepts with the appropriate units. Print out the respective plots and include them in your
lab write-up.
- 9.
- OPTIONAL: Repeat the procedure of item 4 except move from 60 to 20 cm3 as
rapidly as possible and record the pressure data at the start and stop points. Are the
pressure readings consistent with those of the ``slow'' moving experiment? If not can
you suggest a reason?
QUESTIONS:
- I.
- Does the line go through the origin as expected?
By how much should you change the pressure readings so that the line
goes through the origin?
- II.
- What are the possible sources of error in this experiment?
For each source, try to decide what effect it might have on the experimental
results.
- III.
- Read the barometer that is located in your laboratory
room, ask your instructor for help if you are having trouble. Convert the
pressure from cm of Hg to kPa and compare this value with the one
obtained at 60 cm3 in step 5. Is the difference between the two readings important?
Does it affect your conclusions?
- IV.
- OPTIONAL: Assuming that there are 22.4 liters per mole of an ideal gas, how well
does your observed slope agree with your expected slope?
EXPERIMENT II: IDEAL GAS LAW
In this part the Ideal Gas Law is verified by observing the pressure of a fixed volume
of gas at four
different temperatures: Room temperature, 100 oC, 0 oC
and -197 oC. Since PV=nRT and  we can rewrite this as
we can rewrite this as
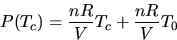
and thereby determine the value of absolute zero (T0) from the intercept.
SUGGESTED PROCEDURE:
- 1.
- CLICK on the telescope icon below to initiate the PASCO
 interface software. The computer, monitor and PASCO interface
must already be on and pressure sensor plugged into the A DIN connector
position. (If not see your instructor.)
interface software. The computer, monitor and PASCO interface
must already be on and pressure sensor plugged into the A DIN connector
position. (If not see your instructor.)
- 2.
- Attach the small stainless steel can (volume
of 98 cm3) as shown below to the PASCO pressure sensor using the plastic ``quick release''
connector. Raise the assembly up if necessary.
Turn on the Fluke thermometer. Unless the stainless steel can has
been recently used it should now be at room temperature.
Figure 2:
Sketch of pressure sensor and stainless-steel can assembly.
![\begin{figure}
\centering
\includegraphics [width=2.8in]{figs/hc1-02.eps}
\vspace*{-.1in}\end{figure}](img359.gif) |
- 3.
- Initiate the data acquisition by clicking on the REC button. There should
be a single plot (temperature vs pressure), a panel meter for pressure and a
keyboard entry window. Record the Fluke meter reading in the keyboard entry window
(if uncertain see EXPT. I, item 5 for a more complete description). Pause the
data acquisition by clicking on the PAUSE button.
- 4.
- Fill the PASCO steam generator with water and turn it on.
The level of the water should be
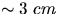 below the top.
Turn the knob to 9 until the water boils and then turn it down somewhat.
below the top.
Turn the knob to 9 until the water boils and then turn it down somewhat.
Figure 3:
PASCO steam generator.
![\begin{figure}
\centering
\includegraphics [width=2.8in]{figs/l103/h02-2.eps}
\vspace*{-.1in}\end{figure}](img361.gif) |
- 5.
- As soon as the water in the steamer is boiling, raise the
pressure sensor stand and then lower it so as to immerse the stainless
steel can in the boiling water.
- 6.
- Wait until the water is boiling again and then put the Fluke
thermometer in the boiling water. Resume the data acquisition by clicking
on the REC button. Watch the pressure readout and after it is stable (with time)
record the Fluke temperature in the data entry window. Turn the PASCO steam generator
off and remove the small stainless steel can from the bath. Pause the data acquisition.
- 7.
- Fill the water jacket container with water and ice. The level of
the water should be
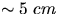 below the top. Repeat the last two steps
for obtaining the 0 oC pressure reading. Empty and dry the stainless steel dewar.
below the top. Repeat the last two steps
for obtaining the 0 oC pressure reading. Empty and dry the stainless steel dewar.
- 8.
- Take the stainless steel dewar and
ask the instructor to fill your dewar with liquid
Nitrogen and repeat step 3 for the container at liquid Nitrogen temperature.
- 9.
- Stop the data acquisition and transfer your
data to a table in your write-up. Do your plot have the correct
functional behavior? Your can refrain from printing out the data until
your have performed a linear regression using either the PASCO graphical
analysis capabilities or the Vernier GA analysis package.
- 10.
- For your curve what is the
expected y intercept?
Now fit this data to a line (using linear regression) and record the slope
and intercepts with the appropriate units.
Print out the plot and include it in your lab write-up.
QUESTIONS
- I.
- What is the percentage difference between the value you found
and the accepted value for absolute zero?
- II.
- Assuming that ice water is exactly at 0 oC and the
boiling water is at 100 oC, estimate the systematic error introduced into
your absolute zero measurement? Does this improve your results?
- III.
- OPTIONAL: Qualitivity what error results from the gas in the small tube not
being always at the can temperature?
- IV.
- OPTIONAL: Does thermal expansion of the can affect your results? In what way?




Next: H-2 Latent Heat
Up: PHYS 201/202 and 207/208
Previous: MC-15b Simple Harmonic Motion and
Michael Winokur
4/7/2000
![]()
![]() ),
and R is the gas constant (
),
and R is the gas constant (![]() ).
). ![]() we can rewrite this as
we can rewrite this as
![]()