



Next: MC-15b Simple Harmonic Motion and
Up: MC-15-Simple Harmonic Motion and
Previous: MC-15-Simple Harmonic Motion and
NOTE TO INSTRUCTORS: This lab uses PASCO rolling carts instead of the more problematic gliders on the air track. The older airtrack version of this lab is MC-15b.
OBJECTIVES:
- 1.
-
To study the period of Simple Harmonic Motion (SHM) as a function of oscillation
amplitude.
- 2.
-
To study the period of SHM as a function of oscillating
mass.
Expected result: Period(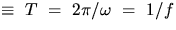 )
)
is proportional to 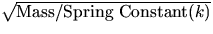
- 3.
-
To demonstrate Hooke's Law, F=-kx
- 4.
-
To observe the relationships between the potential and kinetic energy
THEORY:
The restoring force (F) on an object
attached to a
``simple'' one-dimensional spring is proportional to the
displacement from equilibrium and has the form, F= -k(x-x0), where
k is the spring constant (or stiffness in N/m), x0 is the equilibrium
position (i.e., no net force) and x is the position of the object. This is Hooke's Law. Remember that the simple harmonic oscillator is a good
approximation to physical systems in the real
world, so we want to understand it well. That's the purpose of this lab!
The expression F= ma = -k(x-x0) is a 2nd order differential
equation with
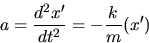
where 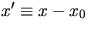 .The most general solution for this expression is often given as
.The most general solution for this expression is often given as
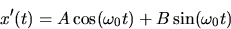
where 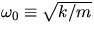 .
.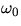 is defined as the natural frequency for the undamped
harmonic oscillator. A and B are arbitrary initial displacement parameters.
Alternatively the solution is often specified as
is defined as the natural frequency for the undamped
harmonic oscillator. A and B are arbitrary initial displacement parameters.
Alternatively the solution is often specified as
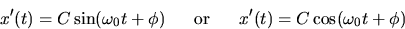
where 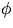 is the starting phase and C is the displacement.
It is also possible to write down these solutions using complex numbers as in
is the starting phase and C is the displacement.
It is also possible to write down these solutions using complex numbers as in
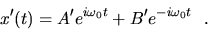
The relative merit of these equivalent expressions will be become clearer
in EXPTS. V and VI.
FUNDAMENTAL CONCEPTS:
- 1.
- The solution to the undamped (i.e., no frictional or drag forces) harmonic
oscillator is time dependent and periodic. When the
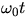 term varies
by
term varies
by 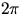 (or one period
(or one period 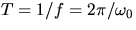 )
both the position, x'(t+T)=x'(t), and velocity, v'(t+T)=v'(t) return to
their previous values.
)
both the position, x'(t+T)=x'(t), and velocity, v'(t+T)=v'(t) return to
their previous values.
- 2.
- Total energy (TE) is conserved in SHM motion. As time evolves kinetic
energy (KE)
is transferred to (and from) potential energy (PE).
Thus at any time t:
![\begin{displaymath}
TE = \mbox{constant} = KE(t) + PE(t) = \frac{1}{2}m [v'(t)]^2 + \frac{1}{2}k
[x'(t)]^2 ~~~~.\end{displaymath}](img307.gif)
APPARATUS:
Basic equipment: PASCO dynamic track, PASCO cart with ``picket fence'', PASCO cart with aluminum plate, adjustable stop, assorted masses, springs: this experiment works best with a pair of short ( 10 mm unstretched length) springs,
timer, photogate & support stand, knife edge assembly.
Computer equipment: Personal computer set
to the MC15a lab manual web-page; PASCO interface module; photogate sensor and
extension jack, PASCO sonic position sensor, speaker with driver stem, power
amplifier module.

PRECAUTIONS:
- 1.
- See MC-14a
- 2.
- When setting up the springs, use the adjustable end stop on the track so the springs are stretched properly: don't stretch them beyond their elastic limit and don't let them sag and drag on the track. Stretching the springs to reach the ends of the track will damage them.
- 3.
- Keep the amplitudes small enough that a
slack spring doesn't touch the track nor a stretched spring exceed its
elastic limit.

SUGGESTIONS: To measure the period of the oscillating cart:
- 1.
- Install a ``picket fence'' on the cart.
- 2.
- Locate the photogate so the black stripe on the fence just cuts off the LED beam (see MC-14a) when the cart is in the
equilibrium position (x-x0 = 0). The photogate phone jack should
be in the first PASCO interface position.
Choose two springs having a similar length and refer to the above precaution.
- 3.
- To initiate the PASCO interface software click the
computer mouse when centered on the telescope icon in the ``toolkit'' area
below. There will be a just a single table for recording the measured period.
- 4.
- Start the cart by displacing it from equilibrium and then releasing
it. Then
start the data acquisition by clicking the REC button button. Let the
cart oscillate for about
10 periods. Calculate the mean and standard deviation by simply
clicking on the statistics icon (i.e.
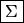 ) on the data table.
) on the data table.
Figure 1:
Sketch of the dynamic track configuration for SHM.
![\begin{figure}
\centering
\includegraphics [width=5.2in]{figs/m15a-01.eps}
\\ \vspace*{-.1in}\end{figure}](img308.gif) |
UNDAMPED SIMPLE HARMONIC MOTION:
- 1.
- Using sketches in your lab book, both at equilibrium and
after a displacement from equilibrium, show that the effective force
constant for 2 identical springs of force constant k on either side of an oscillating
mass is 2k.
- 2.
- EXPERIMENT I: Show experimentally that the
period is independent of the amplitude. Try amplitudes
of approximately 10 cm, 20 cm, and 30 cm. (Friction may be a
problem at very small amplitudes).
- 3.
- EXPERIMENT II: By adding mass to the cart, study the period versus total oscillating
mass. The latter must include a correction for the oscillating springs
whose effective oscillating mass (see the note below) is approximately ms/3
where ms is the mass of the two springs. Explain, in words, how this
correction may be qualitatively justified (Why not ms or ms/2?)
By inspection of your
T vs [M + (ms/3)] curve, what function of T might
yield a straight line when plotted versus [M + (ms/3)]? Prepare this
plot. Calculate the effective force constant, k', (equal to k1+k2, the
two springs will actually differ slightly)
of the system from the slope
of this straight line graph. (Remember
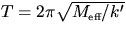 where
where 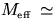 M + ms/3.)
Estimate the uncertainty in k' by solving for k' at each cart mass and
calculating the standard deviation of the mean.
M + ms/3.)
Estimate the uncertainty in k' by solving for k' at each cart mass and
calculating the standard deviation of the mean.
NOTE: Theoretically 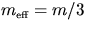 only for
only for
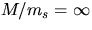 For M = 0, the effective mass is
For M = 0, the effective mass is
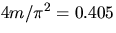 m.
However for M/ms = 5, the effective mass is already
m.
However for M/ms = 5, the effective mass is already 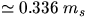 . See
Fig. 1 of J.G. Fox and J. Makanty, American Journal of Physics, 38,
98 (1970).
. See
Fig. 1 of J.G. Fox and J. Makanty, American Journal of Physics, 38,
98 (1970).
- 4.
- EXPERIMENT III : Also measure k directly by hanging the two
springs vertically on a
``knife edge'' assembly in the laboratory. Record the stretch produced by a series
of weights, but do not exceed the elastic limit of either spring! Graph
F vs y for each spring and obtain a best-fit straight line.
The slope should be the spring constant.
Compare this value of k' with that obtained in part #3.
- 5.
- QUESTION: Assuming the spring constant doubles, how would T vary?
FURTHER INVESTIGATIONS OF ``UNDAMPED'' SIMPLE HARMONIC MOTION:
Up to this point you have characterized the SHM of a spring-mass assembly in terms of only a single parameter
T (the period). One of the possible time-dependent expressions for
describing the motion was
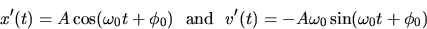
or
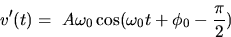
where A is the amplitude (displacement from equilibrium),
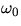 is the natural angular frequency and
is the natural angular frequency and 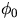 is
the starting phase. Notice that the velocity has a phase shift of
is
the starting phase. Notice that the velocity has a phase shift of
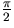 relative to the displacement.
relative to the displacement.
Equally characteristic of SHM is the process of energy transference:
kinetic energy of motion is transferred into potential energy (stored in
the spring) and back again. Friction is an
ever present energy loss process so that the total energy always diminishes
with time.
To capture this rather rapid cyclic process we will again use the
PASCO interface while replacing the photogate sensor with the sonic
position sensor.
EXPERIMENT IV: Measuring the x vs t behavior:
- 1.
- Replace the cart with the picket fence by a cart with an aluminum vane attached to it.
You will want to measure the mass of this new cart and predict the new natural frequency.
Figure 2:
Sketch of the dynamic track with the sonic position sensor.
![\begin{figure}
\centering
\includegraphics [width=5.2in]{figs/m15a-02.eps}
\\ \vspace*{-.1in}\end{figure}](img319.gif) |
- 2.
- Place the position sensor approximately 60 cm from the vane in the
direction of oscillatory motion. Make sure the yellow phone jack is in
the third slot and the black phone jack is in the fourth slot.
Alignment is very important so that the
sensor senses only the vane and not the cart. A slight upward tilt may
help (or raising the vane up slightly as well).
- 3.
- CLICK on the telescope icon below to initiate the PASCO
 interface software.
interface software.
- 4.
- Displace the cart approximately 20 cm from equilibrium to initiate
the oscillatory motion.
CLICK on the the REC button to start your data acquisition. The graph
will simultaneously display both absolute position and velocity versus time.
- 5.
- Practice a few times to make sure you can obtain smoothly varying
sinusoidal curves. Then run the data acquisition for just over ten cycles
and use the cross-hair feature to read out the time increment for ten
full cycles. How does your prediction check out? Determine the initial
phase (i.e., at t=0). Record the equilibrium position (x0) as well.
- 6.
- Use the magnification option of the PASCO software to better view a single
full cycle by clicking on the
magnifying glass icon (in the graph window) and then select two points in the
graph using a CLICK and DRAG motion of the mouse.
- 7.
- Print out (click in graph region and then type ALT, CTRL-P)
or, alternatively, sketch the position and velocity curves in your lab book
identifying key
features in the time dependent curves. In particular identify the characteristic(s)
which demonstrate the
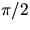 phase difference between the velocity and displacement
curves.
phase difference between the velocity and displacement
curves.
- 8.
- Using the PASCO cross-hair option to read out the relevant time, position and
velocity, make a table as below and fill in the missing entries (identify units).
|
time | phase( 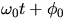 ) ) | x'(t) | v'(t) | KE | PE | TE |
| 0 | | | | | |
| 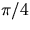 ( 45 deg) ( 45 deg) | | | | | |
| 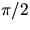 ( 90 deg) ( 90 deg) | | | | | |
| 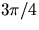 (135 deg) (135 deg) | | | | | |
| 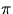 (180 deg) (180 deg) | | | | | |
Figure 2:
Sketch of the dynamic track with the sonic position sensor.
- 9.
- Is the total energy a constant of the motion?
- 10.
- How much displacement amplitude and energy are lost after five full cycles?
What is the approximate friction coefficient?
OPTIONAL INVESTIGATIONS OF ``UNDER-DAMPED'' SIMPLE HARMONIC MOTION:
In the real world friction is an ever present process. In the case of
SHM friction can have a profound effect. Damping of unwanted
vibrations is important in a myriad of situations. (Imagine what driving a
car would be like if there were no shock absorbers!)
Introducing friction can be done by simply adding one more term in the
force expression, 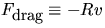 ,
a drag force which is proportional to the velocity where R is the drag coefficient
[units of kg m/s or N/(m/s)] . This is appropriate for motion
thru a viscous fluid but it is really
only a rough approximation for the frictional forces in the track. The modified force expression now becomes
,
a drag force which is proportional to the velocity where R is the drag coefficient
[units of kg m/s or N/(m/s)] . This is appropriate for motion
thru a viscous fluid but it is really
only a rough approximation for the frictional forces in the track. The modified force expression now becomes
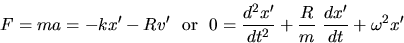
Since energy is continually lost solutions of this expression will be time
dependent but NOT periodic. Adding this ``simple'' term dramatically complicates the
process of finding appropriate solutions. The most general form of the solution
is
![\begin{displaymath}
x' = e^{-(R/2m)t}~~\left[ A e^{+\sqrt{(\frac{R^2}{4m^2}-\ome...
...}~~t} +
B e^{-\sqrt{(\frac{R^2}{4m^2}-\omega_0^2)}~~t}\right] \end{displaymath}](img327.gif)
which is quite formidable.
Since the track drag is low (i.e., R is relatively small) the solution
is said to be underdamped and oscillatory when 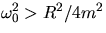 .The solution in this case becomes:
.The solution in this case becomes:
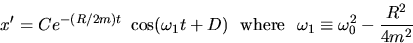
where 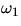 is the natural frequency of the underdamped system and
C and D are the initial displacement and phase.
Because the frequency is lowered, the period lengthens. This is consistent with one's
intuition; drag works against oscillatory motion.
is the natural frequency of the underdamped system and
C and D are the initial displacement and phase.
Because the frequency is lowered, the period lengthens. This is consistent with one's
intuition; drag works against oscillatory motion.
Figure 3:
Sketch of underdamped harmonic motion with 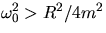 .
.
![\begin{figure}
\centering
\includegraphics [height=2.6in]{figs/m15fig_3.eps}
\\ \vspace*{-.1in}\end{figure}](img331.gif) |
- 1.
- EXPERIMENT V:
- 2.
- CLICK on the telescope icon below to initiate the next PASCO
 interface application. In addition to the graph there will be a ``two'' column
table displaying the time and position then the time and velocity.
interface application. In addition to the graph there will be a ``two'' column
table displaying the time and position then the time and velocity.
- 3.
- Displace the cart approximately 20 cm from equilibrium to initiate
the oscillatory motion.
CLICK on the the REC button to start your data acquisition and record enough
cycles to see the amplitude diminish by two-thirds.
- 4.
- Select six representative times using the table
(identifying where the velocity changes sign) and make a table of t vs maximum displacement.
Use these points in the graphical analysis package and fit these points to the
expression
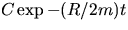 or, in terms of the
explicit analysis formula,
or, in terms of the
explicit analysis formula, ![$y= C *\exp[-B*(x-x_0)]$](img333.gif) .
. - 5.
- How good or poor is the assumption that the drag force is proportional
to the velocity?
- 6.
- Sketch out an approximate curve of x vs t if R were significantly larger.
Which R would be more appropriate for absorbing and dissipating a physical ``shock'' (and
why)?
OPTIONAL INVESTIGATIONS OF RESONANCE:
One of the most important situations of the harmonic oscillator is
that of FORCED, damped harmonic motion. In one-dimension the applied force
is typically sinusoid and when
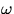 approaches the natural frequency of the system
(nominally
approaches the natural frequency of the system
(nominally 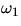 and, if
and, if 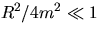 , also
, also
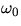 ) the energy of the driver is additively coupled to the moving
mass (e.g., a glider) and resonance occurs.
Resonance is a very important
aspect of the world around us and many mechanical and electronic devices employ
resonant behavior as a fundamental aspect of their operation (e.g., musical
instruments, radios, televisions).
) the energy of the driver is additively coupled to the moving
mass (e.g., a glider) and resonance occurs.
Resonance is a very important
aspect of the world around us and many mechanical and electronic devices employ
resonant behavior as a fundamental aspect of their operation (e.g., musical
instruments, radios, televisions).
Along with the frictional drag (R v' where R is the drag coefficient) one
more force term must be added, that of the mechanical driver, with
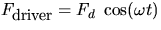 . The new force expression is
conventionally written as:
. The new force expression is
conventionally written as:
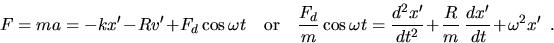
Since the system
energy is lost through friction and may be gained through the driver action,
solutions of this expression will be time dependent but with both
transient and steady-state attributes. In many instances resonant
systems respond so quickly that one only views the steady-state behavior. In
this lab you will be able to observe BOTH the transient and
steady-state processes.
As you may expect the most complete solution of this new differential equation
has a rather complicated form and so is not reproduced here. Since we are
interested only in resonance we can simplify the expression by assuming
solutions that apply to the underdamped case (those with oscillatory behavior).
Thus the analytic solution reduces to:
![\begin{displaymath}
x' = Ce^{-(R/2m)t}~
\cos(\omega_1t+D) + \frac{F_d}{[m^2(\omega_0^2-\omega^2)^2+\omega^2 R^2]^{1/2}}
\cos(\omega t - \phi) \end{displaymath}](img337.gif)
where the first term is the transient behavior,
identical to that of the simple damped harmonic oscillator (described in the
last section) and the second term is the steady-state solution. At
large times t the first terms dies out exponentially so that x' is approximated
by only
![\begin{displaymath}
x'((R/2m)t \gg 1) = \frac{F_d}{[m^2(\omega_0^2-\omega^2)^2+\omega^2 R^2]^{1/2}}
\cos(\omega t - \phi) \end{displaymath}](img338.gif)
where 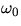 is the natural frequency of the
undamped harmonic oscillator,
is the natural frequency of the
undamped harmonic oscillator, 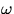 is the mechanical driver frequency,
R is the drag coefficient and
is the mechanical driver frequency,
R is the drag coefficient and 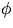 is a measure of the phase difference
between the driver motion and the cart motion.
is a measure of the phase difference
between the driver motion and the cart motion.
In this lab we will only investigate the nature of the cart
displacement with driver frequency (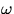 ) in the vicinity of the resonant
frequency. Thus the only relationship of interest becomes
) in the vicinity of the resonant
frequency. Thus the only relationship of interest becomes ![$ x' \propto
[m^2(\omega_0^2-\omega^2)^2+\omega^2]^{-1/2} \equiv Z^{-1/2}$](img339.gif) . Z is a
minimum when the driver frequency is set to
. Z is a
minimum when the driver frequency is set to 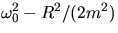 or
or
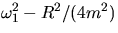 which is
defined to be
which is
defined to be 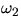 . Since R2/2m2 is small (the PASCO track is a low friction
experiment)
. Since R2/2m2 is small (the PASCO track is a low friction
experiment) 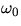 is nearly the same and, in addition, x' will be
sharply peaked about
is nearly the same and, in addition, x' will be
sharply peaked about 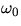 .
.
Figure 4:
Sketch of the relative maximum displacement squared vs
driver frequency.
![\begin{figure}
\centering
\includegraphics [height=2.6in]{figs/m15-04.eps}
\\ \vspace*{-.1in}\end{figure}](img343.gif) |
SUGGESTED PROCEDURE:
- 1.
- EXPERIMENT VI:
Use the rolling cart with the aluminum plate. Weigh the cart and
predict the natural frequency for this new arrangement.
Figure 5:
Sketch of the dynamic track with the position sensor and
speaker.
![\begin{figure}
\centering
\includegraphics [width=5.2in]{figs/m15a-05.eps}
\\ \vspace*{-.1in}\end{figure}](img344.gif) |
- 2.
- Place the position sensor approximately 60 cm from the vane in the
direction of oscillatory motion. Make sure the yellow phone jack is in
the third slot and the black phone jack is in the fourth slot.
Alignment is very important so that the
sensor senses only the vane and not the cart. A slight upward tilt may
help.
- 3.
- Detach the fixed spring end stop and place the speaker as shown in the
figure above with the spring looped through the small slot in the speaker
driver stem using the same considerations for the spring extension as in the
previous experiments.
- 4.
- Make sure the speaker power leads are
plugged into the amplifier module and that its
power is turned on. Also verify that the DIN-9 pin connector (from the
amplifier module) is plugged into the A position in the PASCO interface module.
- 5.
- CLICK on the telescope icon below to initiate the PASCO
 interface software.
interface software.
- 6.
- Make sure the speaker driver window has been switched to the Off
position.
Displace the cart approximately 20 cm from equilibrium to initiate
the oscillatory motion.
CLICK on the the REC button to start your data acquisition. The graph
will simultaneously display glider position and velocity versus time and the
amplifier current (which should be zero).
Practice a few times to make sure you can obtain smoothly varying
sinusoidal curves.
- 7.
- Displace the cart approximately 20 cm from equilibrium to initiate
the oscillatory motion.
CLICK on the the REC button to start your data acquisition and record enough
cycles to see the amplitude diminish by 90%. Compare your data to Fig. 3 and
verify that your cart has a similar transient behavior. Determine the
natural frequency of the system and compare to your prediction.
(This frequency is actually
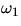 but it is, for this low friction set-up,
nearly the same as either
but it is, for this low friction set-up,
nearly the same as either 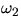 or
or 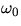 .)
To observe the steady-state properties of resonance you will have to wait
for times longer than those required for this step.
.)
To observe the steady-state properties of resonance you will have to wait
for times longer than those required for this step.
- 8.
- Moving to the PASCO Signal Generator window (shown in Fig. 6),
set the amplifier frequency (which is in Hertz or cycles per second)
to the closest to resonance (0.01 Hz steps) and
engage the speaker but CLICKing
the Auto icon. The driver output should use the sinusoid AC waveform and,
if the overload light on the Power Amplifier flashes on, reduce the voltage
setting slightly. Start the data acquisition (and speaker motion) by
CLICKing on the
REC button and record data until you achieve steady-state behavior.
Figure 6:
Sketch of the PASCO software Signal Generator window.
![\begin{figure}
\centering
\includegraphics [height=2.0in]{figs/s01-08.eps}
\\ \vspace*{-.1in}\end{figure}](img345.gif) |
NOTE: The nominal step sizes for adjusting the amplifier frequecy and voltage
are very large. To reduce the step size depress either
the CTRL key (1 Hz), the ALT key (0.1 Hz), or both (0.01 Hz) while
simultaneously CLICKing the Up or Down arrows.
- 9.
- Set the amplifier frequency 0.01 Hz steps above and below resonance and
record data until you achieve steady-state behavior.
Repeat for 0.10 Hz and
(if time permits) 0.40 Hz steps. Plot out a few representative sets of data.
- 10.
- Determine the maximum steady-state displacement of the cart for each
of the measured frequencies and plot the relative amplitude squared
[(
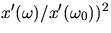 ] vs frequency offset (
] vs frequency offset (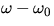 ).
Estimate the full width at half maximum for this curve. This value should
be equal to R/m.
).
Estimate the full width at half maximum for this curve. This value should
be equal to R/m.
- 11.
- Discuss the nature of this resonance curve. If you adjust the R/m ratio
to further sharpen the resonance curve can you identify a compensating
complication if you are interested in achieving steady-state behavior?
If the speaker were attached to an amplifier playing audible music (nominally
20-20,000 Hz), what do you think this the mass will do?




Next: MC-15b Simple Harmonic Motion and
Up: MC-15-Simple Harmonic Motion and
Previous: MC-15-Simple Harmonic Motion and
Michael Winokur
4/7/2000

![\begin{figure}
\centering
\includegraphics [width=5.2in]{figs/m15a-01.eps}
\\ \vspace*{-.1in}\end{figure}](img308.gif)
![\begin{figure}
\centering
\includegraphics [width=5.2in]{figs/m15a-02.eps}
\\ \vspace*{-.1in}\end{figure}](img319.gif)
![\begin{displaymath}
x' = e^{-(R/2m)t}~~\left[ A e^{+\sqrt{(\frac{R^2}{4m^2}-\ome...
...}~~t} +
B e^{-\sqrt{(\frac{R^2}{4m^2}-\omega_0^2)}~~t}\right] \end{displaymath}](img327.gif)
![\begin{figure}
\centering
\includegraphics [height=2.6in]{figs/m15fig_3.eps}
\\ \vspace*{-.1in}\end{figure}](img331.gif)
![\begin{figure}
\centering
\includegraphics [height=2.6in]{figs/m15-04.eps}
\\ \vspace*{-.1in}\end{figure}](img343.gif)
![\begin{figure}
\centering
\includegraphics [width=5.2in]{figs/m15a-05.eps}
\\ \vspace*{-.1in}\end{figure}](img344.gif)
![\begin{figure}
\centering
\includegraphics [height=2.0in]{figs/s01-08.eps}
\\ \vspace*{-.1in}\end{figure}](img345.gif)