



Next: MC-14b Air Track Collisions
Up: MC-14-Elastic and Inelastic Collisions
Previous: MC-14-Elastic and Inelastic Collisions
NOTE TO INSTRUCTORS:
This lab uses PASCO carts and avoids many of the problems of the air track. The older version of this lab that uses gliders on the air track can be found in MC-14b. The three procedures outlined below will certainly take more than the
three hours allotted. Please do procedure I, then as many
of the others as time allows.
OBJECTIVE:
In this experiment you will observe elastic and inelastic collisions between two PASCO carts;
the carts are provided with Velcro bumpers on one end, and magnetic
bumper on the other.
THEORY:
Collisions are a common experience in our lives-the collisions of billiard
balls, the collisions of two football players, the collisions of cars.
Various `natural philosophers' from Galileo onwards discussed the laws that
govern such collisions. As early in the XVIIth century it was understood
that collisions between hard bodies, like billiard balls, behaved differently
from collisions like car wrecks, where the two masses stick together after
the collision. The concept of Momentum was first introduced in mechanics by
Descartes as 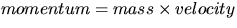 ; he did not get it quite right
however, because he thought of momentum as a scalar quantity.
It was Leibnitz that defined momentum as a vector quantity:
; he did not get it quite right
however, because he thought of momentum as a scalar quantity.
It was Leibnitz that defined momentum as a vector quantity:
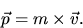
Newton's IInd Law 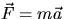 can be rewritten
can be rewritten
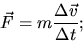
now 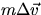 is the change in the quantity
is the change in the quantity
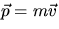 , so one can finally rewrite Newton's IInd law as
, so one can finally rewrite Newton's IInd law as
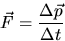
or
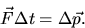
The quantity 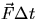 is called the impulse and is equal to
the change in momentum.
is called the impulse and is equal to
the change in momentum.
FUNDAMENTAL CONCEPTS:
A physical quantity is said to be conserved in a process if its
value does not change even though other quantities are changing.
An example of a conserved quantity is energy.
When a body falls freely its total energy (potential energy plus kinetic
energy)remains unchanged while the position and velocity of the body
change with time.
Linear momentum is conserved if
the net force acting on an object is zero. This follows from
the equation which relates the change in momentum to the impulse given
to the object.
Clearly if the force F is zero, the impulse is zero and the
change in momentum is zero, hence the momentum remains constant.
This same principle becomes more useful
when it is applied to an isolated system of
objects. An isolated system is one
where the only forces acting on an object
in the system are due to
the interaction with another object within the same system:
there are no external forces.
A simple such system may consist of two particles, let us call them A and B,
interacting with each other. The force 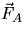 on particle A
is equal and opposite to the force
on particle A
is equal and opposite to the force 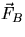 acting on particle B:
acting on particle B:
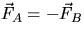 . Because the times during which the forces
act are the same,
it follows that the changes in momentum of the
two particles are also equal and
opposite, so that the total change in momentum is zero.
The conservation of momentum is therefore a consequence of Newton's IIIrd Law.
In the collision of two bodies, the sum of the initial momenta
equals the sum of the final momenta:
. Because the times during which the forces
act are the same,
it follows that the changes in momentum of the
two particles are also equal and
opposite, so that the total change in momentum is zero.
The conservation of momentum is therefore a consequence of Newton's IIIrd Law.
In the collision of two bodies, the sum of the initial momenta
equals the sum of the final momenta:
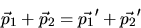
where the unprimed quantities refer to the velocities before the collision,
and the primed quantities refer to the velocities after the collision.
For one dimensional processes the physical quantity
that is conserved
is linear momentum.
A collision is called totally inelastic if the two bodies stick together
after colliding. The conservation of momentum for a one
dimensional totally
inelastic collision is then:
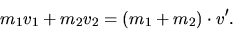
Energy is not conserved in inelastic collisions.
A collision of two bodies is called totally elastic if
energy is conserved in the process. In this case the result of the
collision can be calculated by
(v1-v2) = -(v'1-v'2)'.
It is interesting to note that (v1-v2) and (v'1-v'2) are
the relative velocities of
of body # 1 relative to body # 2 before and after the collision.
APPARATUS:
- 1.
-
Personal Computer with monitor, keyboard, and mouse
- 2.
-
PASCO dynamic track with magnetic bumpers
- 3.
-
PASCO signal interface
- 4.
-
Two PASCO carts with a ``picket fence''
- 5.
-
A set of 500 g masses
- 6.
-
One meter long ruler
- 7.
-
Two photogates: these devices consist of
a source which produces a narrow beam of infrared radiation
an infrared detector at the other side of the gate
that senses the radiation. When the beam between the source and detector is blocked, a red Light Emitting Diode (LED) on the top of the gate lights up; concurrently an electrical signal is sent to the Signal Interface which converts the time during which the beam was blocked into the velocity of the fence. NOTE: for the photogates to work properly, the picket fence must be on the opposite side of the cart closest to the LED.
SUGGESTIONS:
- 1.
- Measure the mass of the empty carts using the pan balance; MAKE
SURE YOU PUT THE CART ON ITS SIDE ON THE PAN. Record these masses in your
lab notebook. Note that the cart with the magnet bumper is somewhat heavier
than the cart without magnet, you may wish to tape some masses on the
lighter cart to equalize the weights.
- 2.
- Initiate the PASCO interface software in the usual way. The monitor should
now look as shown in Figure 1.
Figure 1:
![\begin{figure}
\centering
\includegraphics [width=8cm]{figs/fmc8-1.eps}
\end{figure}](img279.gif) |
-
- On the computer monitor you see a table of velocities for each of the two
photogates. As seen by a person looking at the computer monitor
the photogate on the left is # 1 and the one on the
right is # 2.
- 3.
- Level the track so the carts do not move to the right or the left.
- 4.
- Place the photogates 15 cm apart.
PROCEDURE I - INELASTIC COLLISION - EQUAL MASSES
- 1.
- Prepare a table like the one below:
| Run # | Velocity # 1 (m/s) | Velocity #1 (m/s) |
| | |
|
1 | | |
|
2 | | |
|
3 | | |
Table 1:
- 2.
- Install a picket
fence one cart (on the side opposite the LED). Make sure that it is
the longest
black stripe on the fence that intercepts the LED beam. Put the cart at the
left end of the track.
Place the other
cart just to the
right of photogate #2 as
shown below. Check that the carts do not repel each other;
the Velcro hooks and
loops must be
able to stick together easily.
Figure 2:
![\begin{figure}
\centering
\includegraphics [width=8cm]{figs/fmc8-2.eps}
\end{figure}](img280.gif) |
- 3.
- CLK on REC. Gently push the the projectile cart to
the right toward the first
photogate and the target cart. Catch the carts before they hit the end of the
track. CLK on STOP. Record the velocity of the projectile cart
before and after the collision in Table 1.
- 4.
- Take two more runs.
- 5.
- ANALYSIS OF THE DATA.
Prepare tables as shown below in table 2 and 3.
| Car 1 | Cars 1+2 | |
|
Run # | pini (kg m/s) | pfinal (kg m/s) | 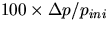 |
| | | |
|
1 | | | |
|
2 | | | |
|
3 | | | |
| | | |
| Avg | | | |
Table 2:
Momentum
| Car 1 | Cars 1+2 | |
|
Run # | Eini (J) | Efinal (J) | 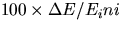 |
| | | |
|
1 | | | |
|
2 | | | |
|
3 | | | |
| | | |
| Avg | | | |
Table 3:
Energy
Calculate the initial and final momenta and enter them in table
2.
Calculate the initial and final kinetic energies and enter them
in table 3
Calculate
and record in table 2 the percent difference in the momenta:
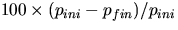 . Calculate
the average percent difference in the momentum.
Calculate
and record in table 3 the percent difference in energy:
. Calculate
the average percent difference in the momentum.
Calculate
and record in table 3 the percent difference in energy:
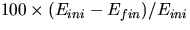 . Calculate
the average percent difference in the energy.
. Calculate
the average percent difference in the energy.
- 1.
- QUESTIONS
What is a reason for the observed difference in momentum?
What fraction of
the energy was dissipated?
What fraction of
the energy should have been dissipated in the absence of friction?
PROCEDURE II - ELASTIC COLLISION - EQUAL MASSES
In this experiment you will be measuring the velocities of two
bodies with equal masses, before and after a totally elastic collision.
- 1.
- Place the photogates about 35cm apart with
one cart just to the left of
photogate #2. Make sure the carts will repel each other.
(One cart has one end
without any magnets-that end will not repel the other cart.) Place the other
cart on the left end of the track. as shown in Fig 3 below.
Cart # 2 should be close to gate # 2, (not as shown in the figure).
Make sure that there is enough space, so that cart #2 starts moving
after cart #1 has passed completely through gate #1.
Figure 3:
![\begin{figure}
\centering
\includegraphics [width=10cm]{figs/fmc8-3.eps}
\end{figure}](img285.gif) |
- 2.
- Prepare a table like table 4.
| Run # | Velocity # 1 (m/s) | Velocity #1 (m/s) |
| | |
|
1 | | |
|
2 | | |
|
3 | | |
| | |
Table 4:
- 3.
- CLK on REC. Gently push the projectile cart (the one
on the left) to the right
toward the first photogate and the target cart. The projectile cart should stop
between the gates and the target will move through photogate # 2. Catch it
before it has time to hit the end of the track; CLK on STOP. Record the
velocities in table 4.
Take two more runs.
- 4.
- ANALYSIS OF THE DATA
Prepare tables like tables 5 and 6.
| Car 1 | Cars 1+2 | |
|
Run # | p1 (kg m/s) | p2 (kg m/s) | 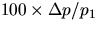 |
| | | |
|
1 | | | |
|
2 | | | |
|
3 | | | |
| | | |
| Avg | | | |
Table 5:
Momentum
| Car 1 | Cars 1+2 | |
|
Run # | E1 (J) | E2 (J) | 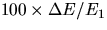 |
| | | |
|
1 | | | |
|
2 | | | |
|
3 | | | |
| | | |
| Avg | | | |
Table 6:
Energy
Calculate the initial momentum of Car # 1 and final momentum
of Car # 2 and enter them in table 5.
Calculate
and record the percent difference of the momenta:
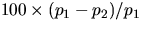 .
Calculate
the average percent difference in the momentum.
Calculate the initial and final kinetic energies and enter them
in table 6.
Calculate
and record the percent difference of the energies:
.
Calculate
the average percent difference in the momentum.
Calculate the initial and final kinetic energies and enter them
in table 6.
Calculate
and record the percent difference of the energies:
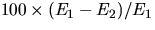 .
. - 5.
- QUESTIONS
What is a reason for the observed difference between p1 and
p2?
What fraction of
the energy was dissipated?
What fraction of
the energy should have been dissipated in the absence of friction?
PROCEDURE III - ELASTIC COLLISION - UNEQUAL MASSES
- 1.
- The
photogates should be about 35cm apart. Find and record the masses of two
500g masses using
the triple beam balance;
place them on the target cart, place this cart just to the left of
photogate # 2 as shown in fig 3 (not as shown in the figure) . The carts should be placed so they will
repel each other.
The lighter cart is `the projectile' and should be placed
on the left end of the track.
- 2.
- Prepare a table like table 7.
| Run # | V1ini (m/s) | V1fin (m/s) | V2fin (m/s) |
| | | |
|
1 | | | |
|
2 | | | |
|
3 | | | |
Table 7:
- 3.
- CLK on REC. Gently push the projectile cart
(the lighter one on the left)
to the right toward the first photogate and the target cart. Try to predict
what will happen. Catch the carts before they hit the end of the track.
CLK on STOP. Record the velocities in Table 7
- 4.
- Take two more runs.
- 5.
- ANALYSIS OF THE DATA
Prepare tables like tables 8 and 9.
| Car 1 ini | Car 1 fin | Car 2 | |
|
Run # | p1ini (kg m/s) | p1fin (kg m/s) | p2fin(kg m/s) | 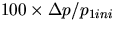 |
| | | | |
|
1 | | | | |
|
2 | | | | |
|
3 | | | | |
| | | | |
| Avg | | | | |
Table 8:
Momentum
| Car 1 ini | Car 1 fin | Car 2 | |
|
Run # | E1ini (J) | E1fin (J) | Efin (J) | 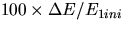 |
| | | | |
|
1 | | | | |
|
2 | | | | |
|
3 | | | | |
| | | | |
| Avg | | | | |
Table 9:
Energy
Calculate the initial and final momentum of each cart
and enter them in
table 8. Calculate the total momentum of the system pfin after the
collision and record it in table 8. Remember that the final momentum
is the sum of the momenta of carts # 1 and # 2 after the collision.
Calculate the initial and final kinetic energies and enter them
in table 9. Calculate the total energy of the system Efin after the
collision and record it in table 9. Remember that the final energy
is the sum of the energies of carts # 1 and # 2 after the collision.
Calculate
and record the percent difference
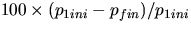 .
Calculate
and record the percent difference
.
Calculate
and record the percent difference
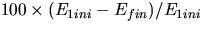 .
.
- 6.
- QUESTIONS
What is a reason for the observed difference?
Was momentum approximately conserved?
What fraction of the energy was dissipated?
What fraction of
the energy should have been dissipated in the absence of friction ?




Next: MC-14b Air Track Collisions
Up: MC-14-Elastic and Inelastic Collisions
Previous: MC-14-Elastic and Inelastic Collisions
Michael Winokur
4/7/2000
![\begin{figure}
\centering
\includegraphics [width=8cm]{figs/fmc8-1.eps}
\end{figure}](img279.gif)
![\begin{figure}
\centering
\includegraphics [width=8cm]{figs/fmc8-2.eps}
\end{figure}](img280.gif)
![\begin{figure}
\centering
\includegraphics [width=10cm]{figs/fmc8-3.eps}
\end{figure}](img285.gif)