The plate P carries a mirror M. The mirror mount has two points resting in a fixed groove, F, and at the other end has a single point resting on the object whose displacement one is measuring. Raising the object through a distance ![]() L will tilt the mirror through an angle
L will tilt the mirror through an angle ![]() or
or
![]() L/d radians (approximately) but will turn the light beam through an angle 2
L/d radians (approximately) but will turn the light beam through an angle 2![]() .
.
![\includegraphics[width=5.7in]{figs/a03-01.eps}](img361.gif)
Figure 1: Schematic of the optical lever.
Hence
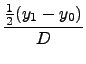
2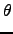 =
= 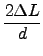 =
= 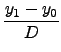 , and
, and 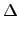 l = (y1 - y0)
l = (y1 - y0)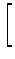
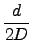
![$\displaystyle \left.\vphantom{ \frac{d}{2D}}\right]$](img368.gif) .
.
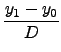 , and
, and
Note that with the telescope nearly perpendicular to the scale at the beginning then y0 is close to the telescope, and the difference between two elongations (
![]() L2 -
L2 - ![]() L1) is very accurately given by
L1) is very accurately given by
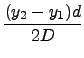
where yi is the scale reading. This relation holds so long as 2![]() is small enough that
tan 2
is small enough that
tan 2![]()
![]() 2
2![]() .
.