![[*]](crossref.gif) .
Please master this material: your instructor is available for help.
.
Please master this material: your instructor is available for help.
OBJECTIVES:
APPARATUS:
INTRODUCTION:
![[*]](crossref.gif) .
Please master this material: your instructor is available for help.
.
Please master this material: your instructor is available for help.
Experiment I. Radius of curvature and focal length of a concave mirror:
|
The Mirror Equation is given by:
|
Figure 1: Layout of concave lens experiment.
|
SUGGESTED PROCEDURE (Note: The mirror holder contains a concave and a convex mirror on opposite sides. Be sure you use the concave mirror!)
|
II. Obtaining f = R/2 by imaging at center of curvature (q = p = R): Replace the illuminated arrow and screen with the rod and place the rod at R. If the tip of the rod is at the center of curvature, a real inverted image will appear just above it with the tip and its image coinciding. An absence of parallax (see parallax) between the tip and image is the most sensitive test for coincidence. When the parallax vanishes, the distance between the tip and the mirror is the radius of curvature R. From several determinations of R, (switching roles with your lab partners estimate the reliability of your results.) |
![\includegraphics[height=2.1in]{figs/l2-02.eps}](img248.gif)
Figure 2: Object and image at center of curvature, R.
|
|
III. By placing object at the principal focus (p = f): If the tip of the rod is at f, rays from the tip will reflect from the mirror as a parallel bundle and give a sharp image of the tip in a telescope focused for parallel rays (see appendix D). Keep the distance between tip and telescope small or the reflected light may miss the telescope. The best test for locating the focal point is absence of parallax between the tip's image and the cross hairs in the telescope, but the telescope must already be focused for parallel rays (e.g., focus on something out the window). From several settings estimate the reliability of your f measurement. |
Figure 3: Object at f, image at infinity.
|
Experiment II: LENSES
1. Converging lens with short focal length:
 +
+ 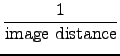 =
= ![\includegraphics[height=1.6in]{figs/l2-04.eps}](img252.gif)
![\includegraphics[height=1.9in]{figs/l2-05.eps}](img253.gif)
![\includegraphics[height=1.6in]{figs/l2-06.eps}](img254.gif)
2. Focal length of a diverging lens:
VIRTUAL PRE-LAB:
![\includegraphics[height=2.0in]{figs/l2-07.eps}](img255.gif)
If using the web-lab manual, launch the virtual application by clicking on the Dual Lens Test Application button below to obverse a point source in action.
As a last step you will move the ``point'' source object (i.e. vary p1 and hence q1) until a sharp image appears in the telescope with no parallax relative to the cross hairs. (This occurs only if parallel rays leave the diverging lens.) The image from the converging lens at q1 serves as a virtual object for the concave lens, Lens2. After properly adjusting p1 this virtual object will be at the focal point of the diverging lens, Lens2. Obtain q1 by setting p1 and using the known value of f1. (Make sure that q1 is large enough to accommodate d + | f2|). Now look for the image in the telescope and adjust p1. Note that since
q2 = ![]() , f2 = p2 and
p2 = d - q1.
, f2 = p2 and
p2 = d - q1.
![\includegraphics[height=2.0in]{figs/l2-08.eps}](img257.gif)
OPTIONAL
Experiment III: Focal Length of a Convex Mirror
Measure the focal length of the convex mirror by combining it with a converging lens. Set the pointed rod at twice the focal length of the lens (p1 = 2f1). Next adjust the mirror position until the inverted image position shows no parallax with the object. Then R = d - 2f1 and
Of course the lens must have f1 > f2, so use a long focal length lens.
![\includegraphics[height=2.2in]{figs/l2-09.eps}](img258.gif)