Reliability estimates of measurements greatly enhance their value. Thus,
saying that the average diameter of a cylinder is
10.00![]() 0.02 mm tells much
more than the statement that the cylinder is a centimeter in diameter.
0.02 mm tells much
more than the statement that the cylinder is a centimeter in diameter.
To physicists the term ``error" is interchangeable with ``uncertainty" and does not have the same meaning as ``mistake". Mistakes, such as ``errors" in calculations, should be corrected before estimating the experimental error. In estimating the reliability of a single quantity (such as the diameter of a cylinder) we recognize several different kinds and sources of error:
FIRST, are actual variations of the quantity being measured, e.g. the diameter of a cylinder may actually be different in different places. You must then specify where the measurement was made; or if one wants the diameter in order to calculate the volume, first find the average diameter by means of a number of measurements at carefully selected places. Then the scatter of the measurements will give a first estimate of the reliability of the average diameter.
SECOND, the micrometer caliper used may itself be in error. The errors thus introduced will of course not lie equally on both sides of the true value so that averaging a large number of readings is no help. To eliminate (or at least reduce) such errors, we calibrate the measuring instrument: in the case of the micrometer caliper by taking the zero error (the reading when the jaws are closed) and the readings on selected precision gauges of dimensions approximately equal to those of the cylinder to be measured. We call such errors systematic, and these cause errors on accuracy.
THIRD, Another type of systematic error can occur in the measurement of a cylinder: The micrometer will always measure the largest diameter between its jaws; hence if there are small bumps or depressions on the cylinder, the average of a large number of measurements will not give the true average diameter but a quantity somewhat larger. (This error can of course be reduced by making the jaws of the caliper smaller in cross section.)
FINALLY, if one measures something of definite size with a calibrated instrument, errors of measurement still exist which (one hopes) are as often positive as negative and hence will average out in a large number of trials. Such errors are called random, and result in less precision. For example, the reading of the micrometer caliper may vary because one can't close it with the same force every time. Also the observer's estimate of the fraction of the smallest division varies from trial to trial. Hence the average of a number of these measurements should be closer to the true value than any one measurement. Also the deviations of the individual measurements from the average give an indication of the reliability of that average value. The typical value of this deviation is a measure of the precision. This average deviation has to be calculated from the absolute values of the deviations, since otherwise the fact that there are both positive and negative deviations means that they will cancel. If one finds the average of the absolute values of the deviations, this ``average deviation from the mean" may serve as a measure of reliability. For example, let column 1 represent 10 readings of the diameter of a cylinder taken at one place so that variations in the cylinder do not come into consideration, then column 2 gives the magnitude (absolute) of each reading's deviation from the mean.
| Measurements | Deviation from Ave. | |
| 9.943 mm | 0.000 | |
| 9.942 | 0.001 | |
| 9.944 | 0.001 | |
| 9.941 | 0.002 | |
| 9.943 | 0.000 | |
| 9.943 | 0.000 | |
| 9.945 | 0.002 | Diameter = |
| 9.943 | 0.000 | |
| 9.941 | 0.002 | 9.943 |
|
|
| |
| Ave = 9.943 mm |
Ave = 0.0009 mm |
Expressed algebraically, the average deviation from the mean
is
= (![]() | xi -
| xi - ![]() |)/n), where xi is the ith
measurement of n taken,
and
|)/n), where xi is the ith
measurement of n taken,
and ![]() is the mean or arithmetic average of the readings.
is the mean or arithmetic average of the readings.
Standard Deviation:
The average deviation shown above is a measure of the spread in a set of
measurements. A more easily calculated version of this is the
standard deviation ![]() (or root mean square deviation). You calculate
(or root mean square deviation). You calculate
![]() by evaluating
by evaluating
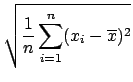
Because of the square, the standard deviation ![]() weights large deviations more heavily
than the average deviation and thus gives a less optimistic estimate of
the reliability. In fact, for subtle reasons involving degrees of freedom,
weights large deviations more heavily
than the average deviation and thus gives a less optimistic estimate of
the reliability. In fact, for subtle reasons involving degrees of freedom,
![]() is really
is really
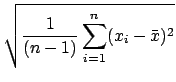
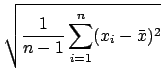
If the error distribution is
``normal" (i.e. the errors, ![]() have a Gaussian distribution,
e-
have a Gaussian distribution,
e-![]() ,
about zero), then on average 68% of a large number of measurements will lie
closer than
,
about zero), then on average 68% of a large number of measurements will lie
closer than ![]() to the true value. While few measurement sets have
precisely a ``normal" distribution, the main differences tend to be in the
tails of the distributions. If the set of trial measurements are generally
bell shaped in the central regions, the ``normal" approximation generally
suffices.
to the true value. While few measurement sets have
precisely a ``normal" distribution, the main differences tend to be in the
tails of the distributions. If the set of trial measurements are generally
bell shaped in the central regions, the ``normal" approximation generally
suffices.
Relative error and percentage error:
Let ![]() be the error in a measurement whose value is a.
Then
(
be the error in a measurement whose value is a.
Then
(![]() ) is
the relative error of the measurement, and
100 (
) is
the relative error of the measurement, and
100 (![]() )% is the
percentage error. These terms are useful in laboratory work.
)% is the
percentage error. These terms are useful in laboratory work.
A.) If the desired result is the sum or difference of two
measurements, the ABSOLUTE uncertainties ADD:
Let ![]() x and
x and ![]() y be the errors in x and y
respectively. For the sum we have
z = x +
y be the errors in x and y
respectively. For the sum we have
z = x + ![]() x + y +
x + y + ![]() y = x + y +
y = x + y + ![]() x +
x + ![]() y
and the relative error is
y
and the relative error is
![]() .
Since the signs of
.
Since the signs of ![]() x and
x and ![]() y
can be opposite, adding the absolute values gives a pessimistic estimate
of the uncertainty. If errors have a normal or
Gaussian distribution and are independent, they combine in quadrature, i.e.
the square root of the sum of the squares, i.e.,
y
can be opposite, adding the absolute values gives a pessimistic estimate
of the uncertainty. If errors have a normal or
Gaussian distribution and are independent, they combine in quadrature, i.e.
the square root of the sum of the squares, i.e.,
For the difference of two measurements we obtain a relative error of
![]() .
which becomes very large if x is nearly equal to y.
Hence avoid, if possible, designing an experiment where one
measures two large quantities and takes their difference to obtain the
desired quantity.
.
which becomes very large if x is nearly equal to y.
Hence avoid, if possible, designing an experiment where one
measures two large quantities and takes their difference to obtain the
desired quantity.
B.) If the desired result involves multiplying (or dividing) measured quantities, then the RELATIVE uncertainty of the result is the SUM of the RELATIVE errors in each of the measured quantities.
Proof:
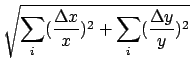
C.) Corollary: If the desired result is a POWER of the measured quantity, the RELATIVE ERROR in the result is the relative error in the measured quantity MULTIPLIED by the POWER: Thus z = xn and
The above results also follow in more general form: Let R = f (x, y, z) be the functional relationship between three measurements and the desired result. If one differentiates R, then
For example, consider the density of a solid (Exp. M1). The relation is
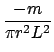
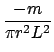 dL.
dL.
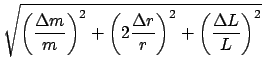
Suppose you have measured the diameter of a circular disc and wish to
compute its area
A = ![]() d2/4 =
d2/4 = ![]() r2. Let the average value of
the diameter be
24.326
r2. Let the average value of
the diameter be
24.326![]() 0.003 mm ; dividing d
by 2 to get r we obtain
12.163
0.003 mm ; dividing d
by 2 to get r we obtain
12.163![]() 0.0015 mm with a relative error
0.0015 mm with a relative error
![]() of
of
![]() = 0.00012.
Squaring r (using a calculator) we have
r2 = 147.938569, with a relative
error
2
= 0.00012.
Squaring r (using a calculator) we have
r2 = 147.938569, with a relative
error
2![]() r/r = 0.00024, or an absolute error in r2 of
0.00024 x 147.93 ... = 0.036
r/r = 0.00024, or an absolute error in r2 of
0.00024 x 147.93 ... = 0.036 ![]() 0.04. Thus we can write
r2 = 147.94
0.04. Thus we can write
r2 = 147.94![]() 0.04, any additional places in r2 being unreliable.
Hence for this example the first five figures
are called significant.
0.04, any additional places in r2 being unreliable.
Hence for this example the first five figures
are called significant.
Now in computing the area
A = ![]() r2 how many digits of
r2 how many digits of ![]() must be
used? A pocket calculator with
must be
used? A pocket calculator with
![]() = 3.141592654 gives
= 3.141592654 gives
A good rule is to use one more digit in
constants than is available in your measurements, and to save
one more digit in computations than the number
of significant figures in the data.
When you use a calculator you usually get many more digits than you need.
Therefore
at the end, be sure to round off the final answer to display the
correct number of significant figures.
SAMPLE QUESTIONS
The htmlscript Quiz System working demo is now available.
Suggestions on Form for Lab Notebooks:
Date performed:____________
Partner:_________________________
Subdivisions:
If appropriate, name and number each section as in the manual.
DATA:
Errors: