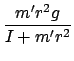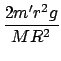OBJECTIVES:
- To study rotational motion resulting from constant torque.
- To investigate the rotational inertia of various objects.
- To experimentally observe the parallel axis theorems.
- If time permits, there is an optional experiment that will demonstrate conservation of angular motion in a ``collision''.
FUNDAMENTAL CONCEPTS OF ROTATIONAL MOTION:
- The equation that describes the rotational motion of an object moving with constant angular velocity are completely analogous to those of linear motion with:
If you make a plot of
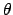 versus t, you find that it describes a straight line. The Greek letter
versus t, you find that it describes a straight line. The Greek letter 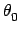 indicates the angular position of the object at time t = 0. The letter
indicates the angular position of the object at time t = 0. The letter 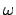 is the slope of the line and this is equal to the angular velocity of the object.
is the slope of the line and this is equal to the angular velocity of the object.
- The equations that describe the rotational motion of an object that
moves with constant angular acceleration are:
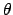 (t) =
(t) = 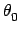 +
+ 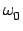 . t +
. t + 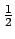
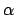 t2 and
t2 and
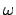 (t) =
(t) = 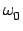 +
+ 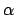 t.
t.
The Greek letter 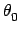 again indicates the angular position of the object at time t = 0.
The letter
again indicates the angular position of the object at time t = 0.
The letter 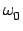 is the the angular velocity of the object at time t = 0, and
is the the angular velocity of the object at time t = 0, and 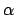 (the angular acceleration) is the slope of the graph of
(the angular acceleration) is the slope of the graph of 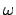 vs t.
vs t.
- It is important to stress that the natural units of angular displacement are in radians and NOT degrees. One full revolution of an object corresponds to 2
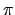 radians or, equivalently, 360o. Typically units for angular velocity are in rad/sec and for angular acceleration are in rad/sec2. Notice that the unit dimensions for equivalent dynamical variables in rotational and linear motion do not match. A linear velocity can never be compared directly with a rotational velocity. Ask your lab instructor for further clarification if this distinction is unclear.
radians or, equivalently, 360o. Typically units for angular velocity are in rad/sec and for angular acceleration are in rad/sec2. Notice that the unit dimensions for equivalent dynamical variables in rotational and linear motion do not match. A linear velocity can never be compared directly with a rotational velocity. Ask your lab instructor for further clarification if this distinction is unclear.
APPARATUS:
- Basic equipment: PASCO rotational assembly; PASCO photogate sensor and support; PASCO super pulley; solid plastic disk; aluminum bar; black metal cylinder; black metal squre; a length of string with metal hooks at both ends; weight hanger and various slotted masses; scale for mass measurements.
- Computer equipment: Personal computer set to the M9 lab manual web-page; PASCO CI 750 or 700 interface module; photogate sensor/smart pulley (this should be plugged into DIGITAL CHANNEL input #3); also a 2nd photogate sensor directly sensing the wheel's rotation (this should be plugged into DIGITAL CHANNEL input #4).
NOTE: If a flywheel needs much more than ten grams on the end of string to maintain constant rotational velocity, notify the instructor.
Pre-lab Quiz
EXPERIMENT I: MEASURING CONSTANT ANGULAR ACCELERATION
(suggested set-up procedures):
- Make sure the PASCO interface has been turned on. If not you may have to reboot the computer. Next make sure that the phone jack connector from the photogate (super pulley) has been plugged DIGITAL channel # 3 position of the PASCO interface module. The computer itself is configured to measure the on/off timing between two adjacent slots in the super pulley wheel and is also calibrated for the pulley's diameter. Thus the read out is in linear velocity of the moving string if it makes non-slipping contact with the pulley.
- Before (as shown in Figure 2, left panel) mounting the solid grey disc hook the wire through one of the holes in the center pulley hub assembly. It will work best if the string is wrapped about the channel formed by the top pulley hub. There are three hubs that one could use but alignment will be easiest with the top one. Unless there is a second hole in the pulley support rod the other two hubs may not line up correctly. Your instructor may wish to demonstrate ``good" winding technique.
- Mount the solid grey disc horizontally onto the rotation shaft as shown in Figure 2.
Figure 2:
The PASCO rotational motion assembly. At left with the solid disc removed and, at right with the disc mounted.
![\includegraphics[height=2.4in]{figs/m9r_2.eps}](img195.gif) |
- 4.
- Make sure the pulley/infrared photogate assembly is properly aligned. As the pulley rotates the little red LED sensor turns off when each slot move past the photogate. More important is make sure that the string runs parallel to the super pulley's channel and the string is tangential to the hub. It may be necessary to rotate the super pulley/photogate assembly.
- 5.
- To initiate the PASCO interface software you will need to click on the telescope icon in the ``toolkit.'' Note that, while you are able to reconfigure the display parameters, the default values that are specified on start-up should allow you to do this experiment without necessitating any major changes. The only value that can be displayed is the linear velocity of the string as it moves and rotates the super pulley. This calibration is fixed and cannot be altered. There is a bogus data set in the starting file. You should delete this before beginning.
- 6.
- Start the PASCO data acquisition by CLICKing on the START icon. To stop the data acquisition CLICK on the STOP icon. (If there are any preexisting data sets you cannot reconfigure either the interface parameters or sensor inputs.)
- 7.
- Using the 50 gram hanger plus another 100 or 150 grams release the disc while a lab partner starts the data acquisition. Stop the data acquisition and the rotating disk before the hanger strikes the floor. Since the torque is constant (see the on-line prelab M9 quiz or paper a copy....this quiz is in lieu of explicitly showing the full calculation) the velocity on screen should increase linearly. Conduct a number of trials to make sure of your technique.
- 8.
- The friction may be small but it is not zero. To extract the net torque you need to subtract off the hanging weight required to overcome friction. Take off the 50 gram weight hanger and suspend two or three grams at a time at the end of the string. When the mass descends with nearly constant velocity that will adequately identify the frictional forces. The mass must be subtracted from the full value. Call this mass m0 and so the effective mass that is available for providing a net accelerating torque is m - m0 or m'.
- 9.
- The plot velocity is proportional to the angular velocity of the wheel and the average acceleration a (i.e., the average slope) is proportional to the angular acceleration
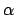 . By using the PASCO plot "zoom select" function (4th icon from left on the graph toolbar), you can magnify and rescale features of interest in the plot display. For the graphical analysis you need to CLICK on the plot window ``Fit" icon and choose the linear function. Your lab instructor can provide assistance if necessary.
. By using the PASCO plot "zoom select" function (4th icon from left on the graph toolbar), you can magnify and rescale features of interest in the plot display. For the graphical analysis you need to CLICK on the plot window ``Fit" icon and choose the linear function. Your lab instructor can provide assistance if necessary.
To obtain the angular acceleration you will need to multiply the linear accelations by the hub's radius r. In principle you could simply measure the radius of the hub with a verier caliper but this would neglect both the string diameter and tracking. A direct measure is a better approach.
DETERMINING THE EFFECTIVE HUB RADIUS:
- (i)
- Align a meter stick vertically from the floor so that you can track the net displacement of the string.
- (i)
- Identify a calibration point on the rim of the grey disc. (Masking tape should work well enough.) Align this near the edge of the meter stick and use the meter stick edge to locate a reproducible starting point.
- (ii)
- Use the weight hanger to identify a height reading. Then lower the string and hanger ten or eleven (or, if using the midde hub, seven or eight) full turns of the wheel and take a second height reading,
- (iii)
- The relationship between the change in height and angle is given by,
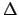 h = r
h = r 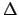
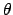 where
where 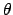 is in radians.
Notice
is in radians.
Notice
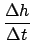 |
= |
r 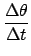 |
|
| v |
= |
r 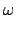 |
|
| dv/dt |
= |
r d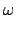 /dt /dt |
|
| a |
= |
r 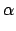 |
|
COMPARING THEORY WITH EXPERIMENT:
Once the effect hub radius is obtained you can directly compare your measured accelerations with those calculated. You will need to measure the mass, M, of the disc (you may neglect the mass and rotational inertia of the center support assembly).
- 1.
- If the mass of the suspended weight is small then you can approximate (see the DERIVATION section and/or on-line quiz) the calculated acceleration by
where
- Let
- I = grey disc moment of inertia (i.e.,
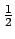 MR2)
MR2)
- m' = effective mass hung on string (m = m0)
- M = mass of grey disc
- r, R = radii of the inner hub and disc, respectively.
- 2.
- For two additional values of masses suspended on the mass hanger obtain their respective average accelerations. Compare the measured accelerations with those calculated. Clearly mark them in your lab manual. How well do they agree?
EXPERIMENT II (MOMENT OF INERTIA and the PARALLEL AXIS THEOREM)
Suggested Procedures:
- Measuring other moments of inertia are no more difficult. In this case it is easy to retain the m'r2 term and rewrite the above equation to give
I =
m'r2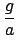
-
m'r2 =
m'r2(
g/
a - 1)
(Once again correcting for friction.)
- 2.
-
The rotational inertia expression for a hollow cylinder (rotating about its axis) is
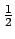 M'(R21 + R22) where R1 and R2 are the inner and outer radii, respectively, and M' is the mass. Place the black metal ring as shown in the adjacent figure and measure the rotational inertia of the two objects. This is simply
Igrey disc + Iblack disk. Compare your calculated and measured values. How well do they
agree? M'(R21 + R22) where R1 and R2 are the inner and outer radii, respectively, and M' is the mass. Place the black metal ring as shown in the adjacent figure and measure the rotational inertia of the two objects. This is simply
Igrey disc + Iblack disk. Compare your calculated and measured values. How well do they
agree?
|
|
- 3.
- Now remove both discs and mount just the
solid grey disk vertically using one of the holes drilled in its side. Experimentally measure the rotational moment of inertia. How does it compare
with that calculated for horizontal mounting case?
- 4.
- Now remove the disc and replace it with the aluminum bar and measure the rotational inertia of the bar. In this case the aluminum bar approximates a thin long rod. Thus
I =
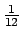 ML2 where M is the mass of the aluminum and L is the overall length. Choose hanging masses that give good reproducibility. Compare your calculated and measure values.
ML2 where M is the mass of the aluminum and L is the overall length. Choose hanging masses that give good reproducibility. Compare your calculated and measure values.
- 5.
- The aluminum bar is designed with a channel that allows you to mount a second object with variable displacements from the rotation axis. Mount a single black rectangular bar (approximately 4.5 cm on
a side) in three position. The first should be centered on the axis of rotation and the latter two approximately 15 cm and 20 cm from the axis of rotation. By the parallel axis theorem,
Im = Ic + mR'2 where Ic is the rotational inertia of the added square black mass m about its own center of mass. So the full express for I is
Ibar + Ic + mR'2.
Plotting I against R'2 should give a straight line. Do your three
points line up?
EXPERIMENT III: CONSERVATION OF ANGULAR MOMENTUM (optional):
- This experiment is designed to mimic the layout of the fourth quiz problem. The problem is: Two uniform density cylinders, one solid (the larger) and one hollow (the smaller) and differing radii are mounted so that the smaller cylinder is held centered and directly above the larger radius mass. Initially the bottom mass is spinning at a uniform angular velocity while the top mass is at rest. You will need to remove the string and hanging mass and use the second rotational sensor directly sensing the angular velocity of the horizontal wheel (see below or on the next page). To conduct this experiment a second PASCO setup file is accessible by clicking on the telescope icon in the web version of the experiment.
- Use the solid grey disk and hollow black disk on the PASCO rotational assembly to recreate this problem. The initial values are:
Li =
Igrey disk 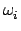
and
Ei =
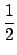 Igrey disk
Igrey disk 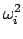
and the final values are:
Lf = (
Igrey disk +
Iblack disk)
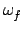
and
Ef =
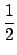
(
Igrey disk +
Iblack disk)
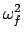
Figure 5:
The PASCO rotational motion assembly with the
photogate reset to measure the angular velocity of the hub directly. Although the
super pulley is not shown it does not need to be removed.
|
![\includegraphics[height=2.4in]{figs/m9r_5.eps}](img209.gif) |
- Move the photogate to the new position and move the plug from Digital Channel
#3 to number #4.
- Slowly spin the grey disc and CLICK on the START icon.
- While the grey disc it spinning hold the top mass (i.e., the black metal ring) just above the spin gray disc. The top mass should be very carefully dropped onto the bottom so that it remains centered and, afterwards, they will ``stick" such that the two masses rotate at the same angular velocity.
- Stop the data acquistion. Repeat the experiment a
few times if necessary.
- Compare the initial and final rotational momenta and energies. How much rotational energy was lost? Were you able to verify conservation of angular momentum? Why or why not?
- NOTE: Before leaving please return the super pulley and
photogate to the original position and switch the plug back to Digital Channel #3.
Michael Winokur
2005-08-30
![\includegraphics[height=2.4in]{figs/m9r_2.eps}](img195.gif)