MY =  =
= 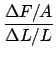
where
 =
= 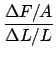
| = | longitudinal force in newtons | ||
| A | = | area in square meters | |
| = | elongation | ||
| L | = | length of wire undergoing the elongation (not the total length!) |
Note that
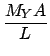
OBJECTIVE:
APPARATUS:
INTRODUCTION:
 =
= 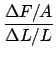
| = | longitudinal force in newtons | ||
| A | = | area in square meters | |
| = | elongation | ||
| L | = | length of wire undergoing the elongation (not the total length!) |
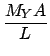
SUGGESTIONS:
PROCEDURE:
 |
QUESTIONS:
Note that the wire fails at a stress which is 100 x less than Young's modulus. Can you understand why the two values are not inconsistent? (Hint: If the stress equaled MY, what would be the strain?).
Could you notice the decrease in diameter of the wire in this experiment by use of a micrometer caliper? If so, try it.