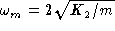Intrinsic Local Modes
Back
Consider a chain of particles of mass m where the nearest-neighbors are connected by the anharmonic springs. The anharmonic interparticle potential has the following form
V = K2 x2 / 2 + K4 x4 / 4 ,
where K2>0 and K4>0 are the harmonic and quartic anharmonic terms, respectively, and x is the deviation of the spring's length from its equilibrium value.

Such lattice supports intrinsic local modes (ILMs) with their frequencies above the phonon band characterized by the maximal harmonic plane waves frequency .
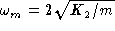The eigenvector of the intrinsic local mode can be found within the rotating-wave apporximation (RWA) where the displacement of the nth particle from its equilibrium position un is described by the following ansatz


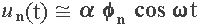
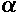where is the amplitude of the mode, and 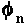characterizes its ac displacement pattern. Substitution of the above ansatz into the classical equations of motion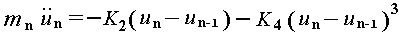

allows one to find the mode eigenvector. The ILM's eigenvector is a wave package which transfers to a lattice envelope soliton in a limit of a weak anharmonicicty.

A similar ansatz can give the eigenvector of a moving ILM.

A more complete description of the intrinsic local modes you can find in a review article:
S. A. Kiselev, S. R. Bickham, and A. J. Sievers, "Properties of Intrinsic Localized Modes in One-Dimensional Lattices", Comments Cond. Mat. Phys, 17, 135-173 (1995).

The above applet allows you to watch vibrating ILMs in the lattice of 15 particles with periodic boundaries. The evolution of the chain is calculated by the molecular-dynamics technique. The parameters of the lattice are the following: m=1, K2=1, K4=10.
You can launch either an Odd-Parity ILM (when a central particle has the highest amplitude) or an Even-Parity ILM (when two central particles have the highest and opposite amplitudes). You can also launch a Moving ILM.

The time is shown in units of the shortest period of small amplitude plane wave vibrations, .

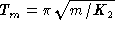Energy is shown in arbitrary units. The kinetic energy of the particle and the potential energy of the bond are shown as the red and the yellow bars, respectively.

If you wait for a while you will see a spectrum of the particles' vibrations. It will be shown in the left panel. As the time of the evolution goes the spectrum resolution improves. The frequency unit is the maximal plane wave frequency, .

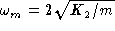Last modified: December 1, 1996
Sergey Kiselev, kiselev@msc.cornell.edu